The history of sphere eversions starts in 1957, when Stephen Smale proved a very general fact about immersions of spheres [Smale 1958]. One consequence of his proof is that there should be a way to turn the sphere inside out by a regular homotopy.
For a little while, this claim met with skepticism. The mathematican Raoul Bott, who had been Smale's graduate adviser and who is one of the founders of differential topology, flatly told Smale that he was wrong, and explained why he thought so. Later he became persuaded that Smale's reasoning was correct, but he, like many other mathematicians, was still frustrated by the inscrutability of Smale's proof, and wished to see a more direct sphere eversion.
``In principle it is possible to piece together the myriad minute geometric constructions prescribed by [Smale's] proof to assemble an explicit visualization of an eversion. This strategy is far from practical'' [Francis 1987]. It is akin to describing what happens to the ingredients of a soufflé in minute detail, down to the molecular chemistry, and expecting someone who has never seen a soufflé to follow this ``recipe'' in preparing the dish.
In 1961, Arnold Shapiro invented the first explicit eversion, but did not publish or divulge it widely. He did explain it to the French mathematician Bernard Morin, who passed it on to his compatriot René Thom, and eventually this eversion became more widely known thanks to Morin and George Francis, and especially to the article [Francis and Morin 1987]. Morin, incidentally, is blind, and the fact that he was one of the first people to understand how a sphere can turn inside out is both a tribute to his ability and a convincing proof that ``visualization'' goes far beyond the physical sense of sight.
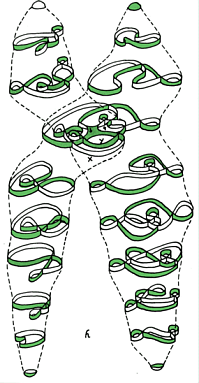
The first time that most mathematicians and the public at large became aware of an explicit eversion was when Tony Phillips, aroused by an exchange of letters with Thom, worked out the details of what he thought was Shapiro's eversion (though later it turned out to be a different one). Phillips published a beautifully written article in Scientific American [Phillips 1966], aimed at a wide audience and culminating with a series of pictures representing various stages of the evolution. Here is one of his original drawings:

The publication of these pictures dispelled the mysterious and paradoxical reputation of the problem; but filling in the missing levels in Phillips' pictures and tracking them through their implied deformations was not an easy task. In fact, a complete mental picture of any eversion is very hard to keep in mind, and clear printed images are even harder to draw, because of the many layers of surface: the most successful expositions of the everting sphere concentrate on local details, and rely on the viewer's powers of synthesis to piece the details together. People began searching for simpler and more symmetrical solutions. Morin, in particular, devised in 1967 a new eversion that was simpler than all the preceding ones in terms of the number of crossings. Charles Pugh made wire-mesh models of various stages of it, and Nelson Max digitized these models and used them as the basis for the movie [Max 1977]. The rendering of the evolving sphere was done by Jim Blinn; here is a frame:
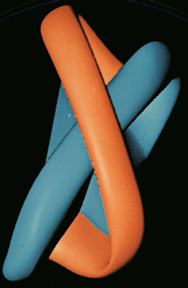
(Shortly after their digitization Pugh's models were stolen from the Berkeley campus, where they had been on display; they have never been recovered, but their digital shadows live on in Max's movie.)
Morin himself described his eversion method in a series of short notes and in a popular-audience article, all skillfully illustrated by Jean-Pierre Petit [Morin and Petit 1978a, 1978b, 1978c, 1980]. One of these notes gave for the first time algebraic equations that might be used for a full-fledged computer rendition of the process.
Morin also found the smallest number and types of ``events'' unavoidable in any eversion. Together with François Apéry, he created a an algebraic-analytic eversion using only the minimal number of events [Apéry 1992]. He also performed a similar feat in the polyhedral realm (where the surfaces of interest are flat-sided rather than smooth), turning a ``sphere'' with twenty triangular sides inside out in the most economical way possible [Morin 1995]. Models for this eversion, made by Richard Denner, are on exhibition at the Palais de la Découverte, in Paris.
In the mid-seventies, Bill Thurston developed his idea of corrugations. This gives another route for the eversion, as explained in Outside In, and it can also be applied to other more general situations.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: May 16, 1995 ---
Last modified: Fri Jun 14 09:48:18 1996
Copyright © 1995-1996 by
The Geometry Center
All rights reserved.