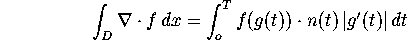Divergence over a Region
The Divergence Theorem says that if a region, D, is bound by a closed curve,
then the integral of the divergence over that region is equal to the
flux across the boundary. This is often written:
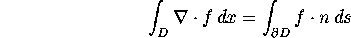 .
.
But what does this mean? Let g(t), t=0..T, parameterize the
boundary in a counter-clockwise fashion. If n(t) is the unit normal to g(t), then we can make sense of the right-hand integral
by writing
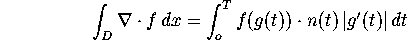
Question #2
In this question we will evaluate the double integral
on the left by computing the line integral on the right.
- Parametrize the unit circle about the stable equilibrium (the sink)
by
g(t), t=0..2*Pi. Note: The sink is not
at the origin!
- Compute the tangent vector g'(t) and use this to
write down the unit normal vector to the circle.
- Use Maple to help you compute the dot product of f(g(t))
and n(t) and the integral of this dot product times the
length of g'(t) from
t=0..2*Pi.
We've provided a hint
in case you get stuck.
Next: The Average Divergence
Up: Introduction
Previous: Divergence at a Point
Frederick J. Wicklin <fjw@geom.umn.edu>
Brian Burt<burt@geom.umn.edu>
Document Created: Wed Jan 25 CST
Last modified: Tue Mar 14 10:27:25 1995
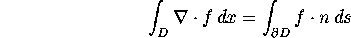 .
.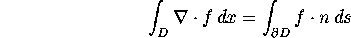 .
.