Article: 125 of geometry.college Newsgroups: geometry.college From: sander@geom.umn.edu (Evelyn Sander) Subject: Squaring the Circle 1 Organization: University of Minnesota, Twin Cities Date: Tue, 21 Dec 1993 20:26:40 GMT Lines: 143The following is a proof that given an arbitrary circle, it is impossible to construct a square of the same area using only straight edge and compass.
People started to try to solve the classical Greek problem of squaring a circle by construction around 200 BC. It was finally proven impossible in 1882, when Lindemann proved that pi was trancendental. (I will omit the proof of this here.) Here are the basic ideas of the proof, following closely the discussion by Courant and Robbins in "What Is Mathematics."
Given an arbitrary circle, let us define our unit of measure to be the radius of the circle. That means that the circle has area pi. Therefore, in order to construct a square of equal area, we need to construct the side of the square, which must have length square root of pi. I show that this is impossible.
First, I must explain what it actually means to say that pi is transendental. This means that pi does not satisfy any rational polynomial equation. In other words, there is no equation of the form a(n)x^n+a(n-1)x^(n-1)+...+a(1)x+a(0)=0 with a's all rational, which holds for x=pi. In particular, this means we cannot find pi by a finite number of applications of the operations of addition, subtraction, multiplication, division, and taking nth roots of rational numbers. Note that it is also impossible to retrieve sqrt(pi) in this way. Now I show that these operations are the only ones available using construction.
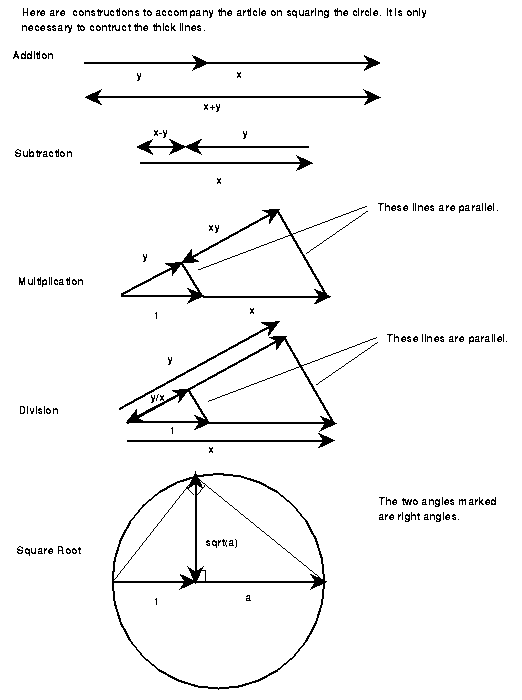
Given segments of lengths x and y, what are all the possible lengths of new segments we can construct? Here are five possibilities: It is possible to make a segment length x+y by lying the two next to each other. Likewise, drawing segment x starting at the right end of y and heading left, the distance from the left endpoint of y to the left endpoint of x is x-y. Through a more sophisticated construction, one can make segments of length xy, x/y, and the square root of x or y. (See accompanying figures.) Thus we can add, subtract, multiply, divide, and take square roots. We can find a right angle to a segment, so in fact, we can think of the five operations as acting on coordinates of points in a coordinate system in the plane.

The five constructions above cover five powerful operations on the coordinates of points in the plane. However, there are other operations not mentioned, such as taking nth roots where n>2, taking trigonometric functions of x and y. Are any additional operations possible by construction? The answer is no. I will show this, and in addition that these five operations are not sufficient to get a segment with length square root of pi.
First I give an exhaustive list of techniques in construction. Then I will show that using this list of techniques, one can only perform the five operations mentioned above.
Using a straight edge, we can:
Given one segment of unit length, the above constructions allow us to reach all points with rational coordinates. Starting with these points with rational coordinates, and using 1-4, what points can we reach?
If two points have rational coordinates (a,b) and (c,d), the line between them, i.e. points solving
x(b-d)-y(a-c)=(bc-ad),
is of the form
jx+ky=m (j, k,m rational).
Given two nonparallel lines of this form:
jx+ky=m andnx+py=q (j,k,m,n,p,q rational),
the lines intersect at the unique point
x=(mp-kq)/(jp-kn),y=(jq-mn)/(jp-kn),
which again has rational coordinates. Thus 1 and 2 do not give any additional points.
A circle with rational center (a,b) through rational point (c,d) are the points solving the equation
(x-a)^2+(y-b)^2=(c-a)^2+(d-b)^2.
This is of the form:
x^2+y^2+jx+ky=m (j,k,m rational)
Given a circle of this form and a line through two points with rational coordinates:
x^2+y^2+jx+ky=m andnx+py=q (j,k,m,n,p,q rational),
their intersection points will be solutions to the quadratic equation, and thus are of the form:
(a+b(sqrt(c)), d+e(sqrt(f))),
where a,b,c,d,e,f are rational. This result follows from the fact that solving for x in the second equation and substituting into the first, we obtain a quadratic equation. Similarly, solving for the intersections of the two circles
x^2+y^2+ax+by=c and x^2+y^2+dx+ey=f (a,b,c,d,e,f rational),
is equivalent to solving for intersections of the system:
x^2+y^2+ax+by=c and(a-d)x+(b-e)y =c-f.
This is intersection of a circle and a line through a point with rational coordinates. We already showed that the result of this intersection. Therefore, the only additional points obtained from 3 and 4 are points with coordinates containing square roots of rational numbers, i.e., coordinates of the form d+e(sqrt(f)) (d,e,f rational).
From the above two paragraphs, we see that starting with rationals, it is only possible by construction to perform the five operations above. In other words, we can only add, subtract, multiply, divide, and take square roots of coordinates to get new coordinates. But we know that it is impossible to ever get the square root of pi from rational numbers in this way. Thus it is impossible find the length of the side of the square of the same area as a given circle.
This proves that it is impossible to square the circle!!
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: May 15 1994 ---
Last modified: Jun 18 1996