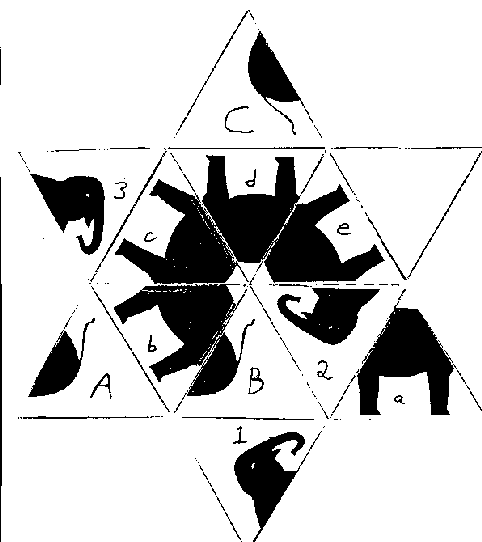

Note that the head faces are labeled with numbers, the body faces are labeled with lowercase letters, the tail faces are labeled with uppercase letters, and the blank face is not labeled at all.
One solution is tail 'A', body 'e', head '1', and the blank face as the bottom side. To get this solution first fold the back of face 'A' onto the back of face 'b'. Next fold the front of face 'a' over the front of face '2', the back of face '2' over the back of face 'B', and then the back of face '1' over the back of face 'a'. After doing these foldings, you should have the following image:
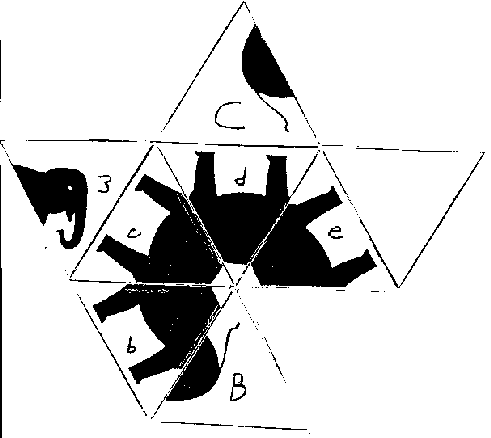
In this picture, the front of faces '1' and 'A' are visible when you flip the paper over.
Next fold the front of face 'b' onto the front of face 'c'. After doing this folding, the three elephant faces that we want are aligned in a row as the following figure shows:
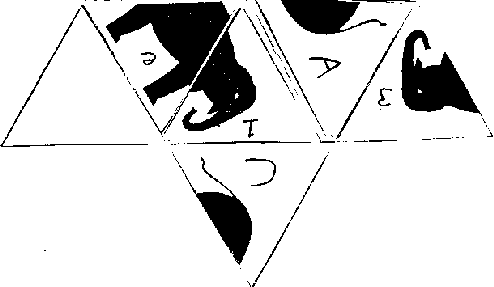
Lastly, fold the back of face '3' over the back of face 'c', the back of face 'C' over the back of face 'd'. Now the foldings are complete, and the remaining four sides on top will fold into a tetrahedron where the head, body and tail connect properly, and the remaining face is a blank.

In my posting of the puzzle, I had two additional questions:
Is there more then one head, body, tail combination?Unfortunately, I have neither a satisfying answer to the first question, nor a complete answer to the second one.How many solutions are there if the blank side must be a blank face?
Yes there is another head, body, tail combination. Again using the notation above tail 'A', body 'd', head '1' with the backside of face '3' is another solution. But this answer is not satisfying to me since it uses the same head and tail as in the described solution above.
If the blank side must be the blank face, then the body 'e' must also be one of the faces in the solution. So far the only solution I can find that allows the inclusion of these two faces is the folding given above.
I think it is possible to answer these questions by listing possible combinations and ruling the impossible ones out. This is the approach Lori Thomson was using to solve the puzzle and how I stumbled upon an answer. For instance if we list all of the head and tail combinations we get nine possiblilities:
1ABoth 1B and 2B can be immediately ruled out as possibilities, since the head and tail combinations share an edge which forces the faces to be aligned improperly. Also 2A and 3A appear to be impossible combinations. After that I'm not sure if any other combinations can be ruled out. So to try and answer this puzzle, I would next list and consider the head and body combinations, and then body and tail combinations. Hopefully this systematic listing and ruling out combinations we leave only a small set to consider.
2A
3A
1B
2B
3B
1C
2C
3C
Does anyone have a more elegant way of finding solutions? Although I sometimes enjoy doing things that involve brute force, I would love to see a slicker approach to the puzzle.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: July 11 1995 ---
Last modified: Jun 18 1996