Distance recipe
Next: A field guide
Up: Geometry and the Imagination
Previous: Hyperbolic Geometry
Here is a technical definition of how to compute distance.
Begin with any two points. If 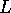 is the
is the 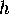 -line on which they lie,
let
-line on which they lie,
let 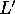 be the line on the back hemisphere that projects onto
be the line on the back hemisphere that projects onto 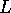 .
Rotate the sphere so that one of the end points of
.
Rotate the sphere so that one of the end points of 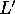 moves to the north
pole,
moves to the north
pole, 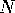 .
.
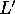 rotates into a new line
rotates into a new line 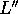 passing through
passing through 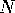 . The projection
of
. The projection
of 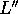 is now a vertcal line,
is now a vertcal line, 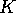 . The points
. The points  and
and 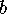 have been
lifted to
have been
lifted to 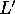 rotated to
rotated to 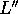 and then projected onto
and then projected onto 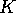 . They are now
called
. They are now
called 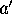 and
and 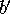 . We can take the ratio of the heights of
. We can take the ratio of the heights of 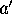 and
and 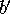 .
This is almost a distance. However, distance should be
symmetric. The ratio of the heights depends upon which point we name first.
Therefore, we take the absolute value of the natural log of the ratio of the heights to be
the distance between
.
This is almost a distance. However, distance should be
symmetric. The ratio of the heights depends upon which point we name first.
Therefore, we take the absolute value of the natural log of the ratio of the heights to be
the distance between  and
and 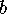 .
.
Consider the two pairs of points
To our Euclidean eyes it appears to us that 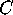 and
and 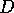 are twice as far
apart as
are twice as far
apart as 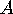 and
and 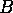 . When we put on our hyperbolic glasses,
we realize that the distance between
. When we put on our hyperbolic glasses,
we realize that the distance between 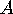 and
and 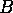 is exactly the same
as the distance between
is exactly the same
as the distance between 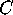 and
and 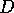 .
.
Let 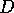 be the unit disc in the plane.
be the unit disc in the plane.  .
We saw earlier that
.
We saw earlier that  is the image of the lower half sphere under
stereographic projection. This is another model for the hyperbolic plane.
We will easily locate the h-lines once we see how this is related to
the upper half-plane.
is the image of the lower half sphere under
stereographic projection. This is another model for the hyperbolic plane.
We will easily locate the h-lines once we see how this is related to
the upper half-plane.

Figure 24: Some h-lines in 
Take the sphere. Rotate it so that the back hemisphere goes
into the bottom hemisphere. Project the bottom hemisphere onto the unit
disc. This procedure identifies the upper half plane (the image of the
back hemisphere) with the unit disc (the image of the bottom hemisphere).
An h-line in the upper half plane corresponds to a circle on the back
hemisphere which is perpendicular to the prime meridian. Such a circle rotates
into a circle on the bottom hemisphere that is perpendicular to the
equator, and then projects to a circle in the plane that intersects the
boundary of the unit disc at right angles.
When we project onto the unit
disc, we no longer have to worry about h-lines through infinity.
Things look much more symmetric. However, we still have one weird
type of h-line: a Euclidean straight line passing through the center of the
disc. (See figure 24.)

Figure 25: Some hyperbolic cloth: A tiling of the hyperbolic plane by triangles with angles 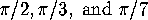
Once we have a hyperbolic geometry, many new things are possible.
- We can classify patterns on hyperbolic cloth.
We can look for hyperbolic mirrors, hyperbolic gyration points, etc.
and analyze hyperbolic cloth just as we analyzed Euclidean cloth.
- We can form a
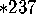 orbifold.
orbifold.
Enclosed is a picture of the tiling of the hyperbolic plane by triangles
whose angles are 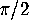 ,
, 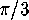 and
and 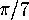 . (See figure 25.)
The important thing to realize
about this picture is that ALL the trianglular tiles are congruent. That is,
even though the triangles near the boundary of
. (See figure 25.)
The important thing to realize
about this picture is that ALL the trianglular tiles are congruent. That is,
even though the triangles near the boundary of  appear to be much
smaller than those in the center, their sides all have the same lengths.
To see this you just have to look through your hyperbolic glasses.
appear to be much
smaller than those in the center, their sides all have the same lengths.
To see this you just have to look through your hyperbolic glasses.
Next: A field guide
Up: Geometry and the Imagination
Previous: Hyperbolic Geometry
Peter Doyle
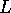 is the
is the  -line on which they lie,
let
-line on which they lie,
let 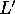 be the line on the back hemisphere that projects onto
be the line on the back hemisphere that projects onto 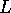 .
Rotate the sphere so that one of the end points of
.
Rotate the sphere so that one of the end points of 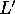 moves to the north
pole,
moves to the north
pole, 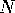 .
.
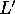 rotates into a new line
rotates into a new line 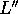 passing through
passing through 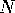 . The projection
of
. The projection
of 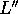 is now a vertcal line,
is now a vertcal line, 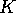 . The points
. The points  and
and 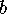 have been
lifted to
have been
lifted to 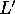 rotated to
rotated to 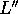 and then projected onto
and then projected onto 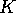 . They are now
called
. They are now
called 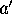 and
and 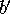 . We can take the ratio of the heights of
. We can take the ratio of the heights of 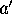 and
and 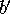 .
This is almost a distance. However, distance should be
symmetric. The ratio of the heights depends upon which point we name first.
Therefore, we take the absolute value of the natural log of the ratio of the heights to be
the distance between
.
This is almost a distance. However, distance should be
symmetric. The ratio of the heights depends upon which point we name first.
Therefore, we take the absolute value of the natural log of the ratio of the heights to be
the distance between  and
and 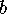 .
.
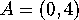 and
and 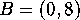 .
.
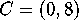 and
and 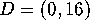 .
.
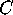 and
and 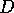 are twice as far
apart as
are twice as far
apart as 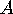 and
and 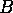 . When we put on our hyperbolic glasses,
we realize that the distance between
. When we put on our hyperbolic glasses,
we realize that the distance between 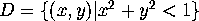 .
We saw earlier that
.
We saw earlier that 

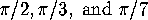
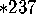 orbifold.
orbifold.
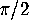 ,
, 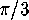 and
and 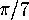 . (See figure
. (See figure