Stereographic Projection
Next: The orbifold shop
Up: Geometry and the Imagination
Previous: Names for symmetry
We let 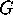 be a sphere in Euclidean three space. We want to obtain
a picture of the sphere on a flat piece of paper or a plane.
Whenever one projects a higher dimensional object onto a lower dimensional object, some type of distortion must occur. There are a number of different ways to project and each projection preserves some things and distorts others.
Later we will explain why we choose stereographic
projection, but first we describe it.
be a sphere in Euclidean three space. We want to obtain
a picture of the sphere on a flat piece of paper or a plane.
Whenever one projects a higher dimensional object onto a lower dimensional object, some type of distortion must occur. There are a number of different ways to project and each projection preserves some things and distorts others.
Later we will explain why we choose stereographic
projection, but first we describe it.
We shall map the sphere 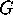 onto the plane containing its equator.
Connect a typical point
onto the plane containing its equator.
Connect a typical point 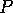 on the surface of the sphere to the north pole
on the surface of the sphere to the north pole 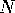 by a straight line in three space. This line will intersect the equatorial plane at some point
by a straight line in three space. This line will intersect the equatorial plane at some point 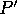 . We call
. We call 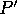 the projection of
the projection of 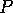 .
.
Using this recipe
every point of the sphere except the North pole projects to some point on the equatorial plane. Since we want to include the North pole in our picture, we add an extra point 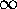 , called
the point at infinity, to the equatorial plane
and we view
, called
the point at infinity, to the equatorial plane
and we view  as the image of
as the image of  under stereographic projection.
under stereographic projection.
Stereographic projection preserves circles and angles.
That is, the image of a circle on the sphere is a circle in the plane and the angle between two lines on the sphere is the same as the angle between their images in the plane. A projection that preserves angles is called a conformal projection.
We will outline two proofs of the fact that stereographic projection preserves
circles, one algebraic and one geometric. They appear below.
Before you do either proof, you may want to clarify in
your own mind what a circle on the surface of a sphere is.
A circle lying on the sphere is the intersection of a plane in three space with the sphere.
This can be described algebraically.
For example, the sphere of radius 1 with center at the origin is given by
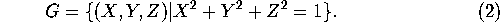
An arbitrary plane in three-space is given by
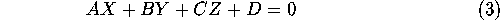
for some arbitrary choice of the constants 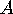 ,
,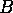 ,
,
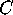 , and
, and 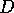 .
Thus a circle on the unit sphere is any set of points whose coordinates
simultaneously satisfy equations 2 and 3.
.
Thus a circle on the unit sphere is any set of points whose coordinates
simultaneously satisfy equations 2 and 3.
The fact that the points 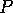 ,
, 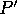 and
and 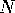 all lie on one line can be expressed by the fact that
all lie on one line can be expressed by the fact that
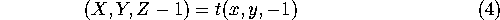
for some non-zero real number 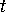 . (Here
. (Here 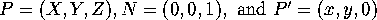 .)
.)
The idea of the proof is that one can
use equations 2 and 4 to write 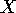 as a function of
as a function of 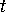 and
and 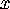 ,
, 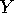 as a function of
as a function of 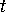 and
and 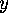 , and
, and 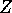 as a function of
as a function of 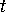 and
to simplify equation 3 to an equation in
and
to simplify equation 3 to an equation in 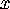 and
and 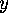 .
Since the equation in
.
Since the equation in 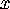 and
and 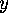 so obtained is clearly the equation of a circle in the
so obtained is clearly the equation of a circle in the 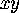 plane, the projection of the intersection of 2 and 3 is a circle.
plane, the projection of the intersection of 2 and 3 is a circle.
To be more precise:
Equation 4 says that 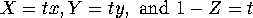 .
Set
.
Set 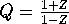 and verify that
and verify that
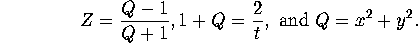
If

lies on the plane,
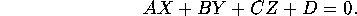
Thus
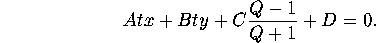
Or
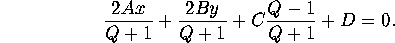
Whence,
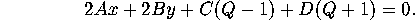
Or
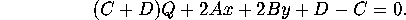
Recalling that

, we see
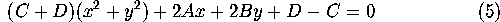
Since the coefficients of the

and the

terms are the same, this is
the equation of a circle in the plane.
The geometric proofs sketched below use the following principle:
It doesn't really make much difference if instead of projecting onto
the equatorial plane, we project onto another horizontal plane (not
through N), for example the plane that touches the sphere at the South
pole, S. Just what difference does this make?
- Angles:
To see that stereographic projection preserves angles at
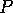 , we
project onto the horizontal plane
, we
project onto the horizontal plane 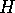 through
through 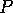 . Then by symmetry
the tangent planes
. Then by symmetry
the tangent planes 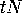 and
and 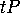 at
at 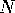 and
and 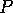 make the same angle
make the same angle 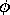 with
with 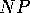 , as also does
, as also does 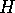 , by properties of parallelism (see figure # 1 at the end of this handout).
, by properties of parallelism (see figure # 1 at the end of this handout).
So 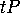 and
and 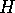 are images of each other in the (``mirror'') plane
are images of each other in the (``mirror'') plane 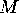 through
through 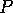 and perpendicular to
and perpendicular to 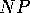 .
.
For a point 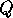 on the sphere near
on the sphere near 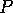 , the line
, the line 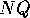 is nearly parallel to
is nearly parallel to 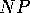 , so that for points near
, so that for points near 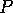 , stereographic projection is approximately
the reflection in
, stereographic projection is approximately
the reflection in 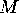 .
.
- Circles: To see
that stereographic projection takes circles to circles, first
note that any circle
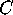 is where some cone touches the sphere, say the cone
of tangent lines to the sphere from a point
is where some cone touches the sphere, say the cone
of tangent lines to the sphere from a point 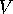 .
.
Now project onto the horizontal plane 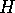 through
through 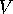 .
.
In figure # 2 which NEED NOT be a vertical plane,
the four angles 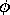 are equal, for the same reasons as before, so that
are equal, for the same reasons as before, so that
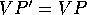 . The image of
. The image of 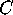 is therefore the horizontal circle of the
same radius centered at
is therefore the horizontal circle of the
same radius centered at 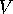 .
.
- Inversion: Another proof uses the fact that
stereographic projection may be
regarded as a particular case of inversion in three dimensions. You
might like to prove that inversion preserves angles and circularity
in two dimensions. The inverse of a point
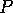 in the
circle of radius
in the
circle of radius 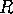 centered at
centered at 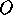 is the unique point
is the unique point 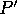 on the
ray
on the
ray 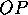 for which
for which 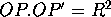 .
.
Next: The orbifold shop
Up: Geometry and the Imagination
Previous: Names for symmetry
Peter Doyle
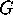 be a sphere in Euclidean three space. We want to obtain
a picture of the sphere on a flat piece of paper or a plane.
Whenever one projects a higher dimensional object onto a lower dimensional object, some type of distortion must occur. There are a number of different ways to project and each projection preserves some things and distorts others.
Later we will explain why we choose stereographic
projection, but first we describe it.
be a sphere in Euclidean three space. We want to obtain
a picture of the sphere on a flat piece of paper or a plane.
Whenever one projects a higher dimensional object onto a lower dimensional object, some type of distortion must occur. There are a number of different ways to project and each projection preserves some things and distorts others.
Later we will explain why we choose stereographic
projection, but first we describe it.
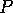 on the surface of the sphere to the north pole
on the surface of the sphere to the north pole 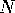 by a straight line in three space. This line will intersect the equatorial plane at some point
by a straight line in three space. This line will intersect the equatorial plane at some point 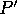 . We call
. We call 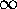 , called
the point at infinity, to the equatorial plane
and we view
, called
the point at infinity, to the equatorial plane
and we view 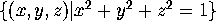 so that
so that  plane is the equatorial plane. The typical point
plane is the equatorial plane. The typical point  . The typical point
. The typical point  , will be called
, will be called 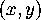 .
.
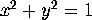 .
.
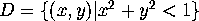 .
.
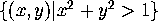 .
.
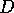 or exterior to it?
or exterior to it?
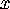 -axis?
-axis?
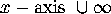 ?
Call the set of points that project onto
?
Call the set of points that project onto 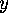 -axis?
onto any vertical line, not necessarily the
-axis?
onto any vertical line, not necessarily the 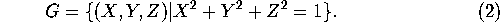
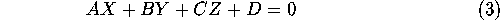
 ,
, ,
,
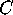 , and
, and 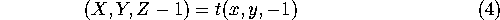
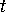 . (Here
. (Here 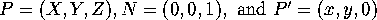 .)
.)
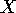 as a function of
as a function of 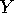 as a function of
as a function of 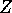 as a function of
as a function of 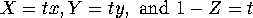 .
Set
.
Set 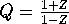 and verify that
and verify that
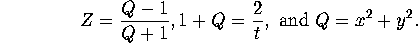

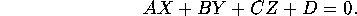
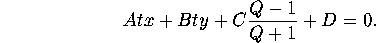
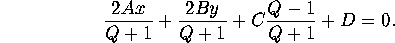
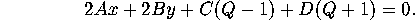
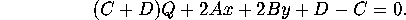

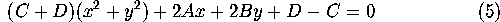


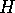 through
through 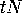 and
and 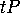 at
at 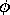 with
with 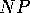 , as also does
, as also does 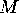 through
through 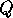 on the sphere near
on the sphere near 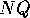 is nearly parallel to
is nearly parallel to 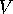 .
.
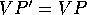 . The image of
. The image of 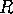 centered at
centered at 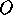 is the unique point
is the unique point 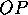 for which
for which 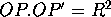 .
.