Next: The Geometry Center's 6-foot icosahedron
Up: Table of Contents
Prev: Assembling the structure
Exercise: How big is Your Icosahedron?
Ask the students to measure or calculate how large their icosahedron is.
This may generate a discussion about what we mean by "how large."
The icosahedron has both a "long diameter" (from one vertex to the
opposite vertex) and a "short diameter" (from one face to the
opposite face). Can the students relate these quantities to inscribed
and circumscribed spheres?
The "long diameter" (widest part) of an
icosahedron may be calculated from the edge length of the icosahedron.
It turns out that the diameter is
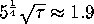
times larger than the side length, where
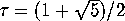
is a constant called the "golden mean." Can
the students derive this quantity (very hard, especially if the students
aren't familiar with trigonometry!) or experimentally determine the
quantity by measuring the diameters and edge lengths of several icosahedra?
Can the students calculate the surface area of the icosahedra? What
about obtaining an estimate of volume? Estimating the radius of
inscribed and circumscribed spheres may help the students provide an
upper and lower bound on the volume.
Next: The Geometry Center's 6-foot icosahedron
Up: Table of Contents
Prev: Assembling the structure
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Author: Frederick J. Wicklin <fjw@geom.umn.edu>
Comments to:
webmaster@www.geom.uiuc.edu
Created: Summer 1994 ---
Last modified: Jul 21 1996
Copyright © 1994-1996 by
The Geometry Center
All rights reserved.
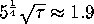
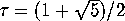
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page