Hyperbolic Geometry
Next: Distance recipe
Up: Geometry and the Imagination
Previous: Positive and negative
When we tried to make a closed polyhedron by snapping together
seven equilateral triangles so that there were seven at every
vertex, we were unable to do so.
Those who persisted and continued to snap together seven
triangles at each vertex, actually constructed an approximate
model of the hyperbolic plane. It is this bumpy sheet with angular excesses all over the place that you
might think of when you try to visualize the hyperbolic plane.
Since we know that angular excess corresponds to negative curvature, we
see that
the hyperbolic plane is a negatively curved space.
Hyperbolic geometry is also known as Non-Euclidean geometry.
The latter name reflects the fact that it was originally discovered by
mathematicians seeking a geometry which failed to satisfy Euclid's parallel
postulate. (The parallel postulate states that through any point
not on a given line there is precisely one line
that does not intersect the given line.) While we will outline the details
of Non-Euclidean geometry and prove that it fails to satisfy the parallel postulate, our main emphasis will be on the feel of the hyperbolic
plane and hyperbolic 3-space.
There are a number of different models for the hyperbolic plane.
They are, of course, all equivalent. As with any instance when
there are several ways to describe something, each description has
both advantages and disadvantages. We will describe two
models, the upper half-plane model, which we denote by U
and the unit disc
model, which we initially denote by D.
It will generally be clear from the context which
model we are using. Although we first present the upper
half-plane model and prove most of the fundamental facts there, we will
generally
after that use the unit disc.
Remember that the image of
the back hemisphere under stereographic projection is the set of all
points in the 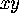 plane whose
plane whose 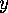 is positive. This is the upper half-plane. The prime
meridian projects onto the line
is positive. This is the upper half-plane. The prime
meridian projects onto the line 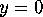 to which we have added
the point at infinity. We think of the image of the prime meridian as the boundary of the upper half-plane. The line
to which we have added
the point at infinity. We think of the image of the prime meridian as the boundary of the upper half-plane. The line 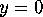 could be referred to as the
could be referred to as the 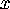 axis.
We will also refer to it as the real axis,
axis.
We will also refer to it as the real axis, 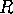 .
.

Figure 22: Some h-lines in the upper half-plane.
To define a geometry in 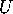 we need to define what is meant by a
straight line through two points.
Given two points
we need to define what is meant by a
straight line through two points.
Given two points 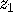 and
and 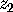 in
in 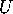 , one can construct many circles
passing through both of them since three points determine a circle.
However, there is a unique circle
passing through
, one can construct many circles
passing through both of them since three points determine a circle.
However, there is a unique circle
passing through 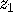 and
and 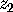 that is perpendicular to
that is perpendicular to 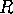 . We call
this circle the straight line passing through
. We call
this circle the straight line passing through 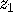 and
and 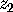 .
When we want to
emphasize that we are talking about the hyperbolic line through
two points rather than the Euclidean line, we refer to it as an h-line.
.
When we want to
emphasize that we are talking about the hyperbolic line through
two points rather than the Euclidean line, we refer to it as an h-line.
You will notice that if 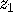 and
and 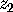 lie on a vertical line, then
there is no Euclidean circle through both that is perpendicular to the boundary.
However, recall that a circle
on the sphere that passes through the north pole projects onto a what at first glance looks like a line, but is upon reflection can be viewed as a circle (it passes through infinity where it closes up.). We shall also view this line as a circle.
lie on a vertical line, then
there is no Euclidean circle through both that is perpendicular to the boundary.
However, recall that a circle
on the sphere that passes through the north pole projects onto a what at first glance looks like a line, but is upon reflection can be viewed as a circle (it passes through infinity where it closes up.). We shall also view this line as a circle.
Thus an h-line is either a circle perpendicular to the real axis
or a vertical line (see figure 22).
(The latter is also automatically perpendicular to the real axis.)
(As a homework exercise you can remind yourself
that any circle that intersects the real axis at right angles
has its center on the real axis.)
We note that two Euclidean circles are either disjoint, intersect in a point,
or intersect in two points. Two circles whose centers are on the
real axis that intersect in two points have one point of intersection
above the real axis and one below. Thus they have only one point of
intersection in the upper half-plane. Similarly, a circle with center
on the real axis and a vertical line can have at
most one point of intersection in the upper half-plane.
Thus any two h-lines are either disjoint or intersect in a point.
We have now proved that this system of lines and points
satsifies two of the axioms for a geometry.

Figure 23: Several h-lines through 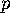 that are disjoint from
that are disjoint from 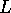 .
.
- What does a hyperbolic mirror look like?
- What does a hyperbolic mirror
string look like?
- What is the maximum number of mirrors in a Euclidean mirror string?
- What is the maximum number of mirrors in a hyperbolic mirror string?
We turn to the parallel axiom. Again let 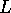 be any h-line. For the sake of
simplicity assume that
be any h-line. For the sake of
simplicity assume that 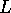 is not a vertical h-line. Let
is not a vertical h-line. Let 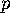 be any point
not on
be any point
not on 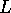 .
We can construct a whole family of Euclidean circles whose centers
are on the real axis which pass through
.
We can construct a whole family of Euclidean circles whose centers
are on the real axis which pass through 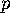 and which do not intersect
and which do not intersect
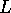 . Figure 23 illustrates several such h-lines.
For homework, you can work out either one example or a detailed proof.
. Figure 23 illustrates several such h-lines.
For homework, you can work out either one example or a detailed proof.
We have emphasized that one of the main distinctions between
geometry and topology is that distance is intrinsic to geometry.
Thus it behooves us to define a distance in the hyperbolic plane. Again, our
emphasis should not be on computing distance, but on having a
feel for hyperbolic distance. The important fact to remember is:
-
Line segments that appear to be of very different lengths
to our Euclidean eyes may be of the same length when we wear
hyperbolic glasses and vice-versa.
Next: Distance recipe
Up: Geometry and the Imagination
Previous: Positive and negative
Peter Doyle
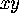 plane whose
plane whose 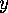 is positive. This is the upper half-plane. The prime
meridian projects onto the line
is positive. This is the upper half-plane. The prime
meridian projects onto the line 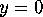 to which we have added
the point at infinity. We think of the image of the prime meridian as the boundary of the upper half-plane. The line
to which we have added
the point at infinity. We think of the image of the prime meridian as the boundary of the upper half-plane. The line 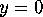 could be referred to as the
could be referred to as the 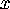 axis.
We will also refer to it as the real axis,
axis.
We will also refer to it as the real axis, 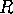 .
.

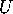 we need to define what is meant by a
straight line through two points.
Given two points
we need to define what is meant by a
straight line through two points.
Given two points 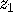 and
and 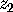 in
in 
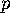 that are disjoint from
that are disjoint from 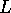 .
.