 's and
's and
 's.
's.
If you take a flat piece of paper and bend it gently, it bends in only one direction at a time. At any point on the paper, you can find at least one direction through which there is a straight line on the surface. You can bend it into a cylinder, or into a cone, but you can never bend it without crumpling or distorting to the get a portion of the surface of a sphere.
If you take the skin of a sphere, it cannot be flattened out into the plane without distortion or crumpling. This phenomenon is familiar from orange peels or apple peels. Not even a small area of the skin of a sphere can be flattened out without some distortion, although the distortion is very small for a small piece of the sphere. That's why rectangular maps of small areas of the earth work pretty well, but maps of larger areas are forced to have considerable distortion.
The physical descriptions of what happens as you bend various surfaces without distortion do not have to do with the topological properties of the surfaces. Rather, they have to do with the intrinsic geometry of the surfaces. The intrinsic geometry has to do with geometric properties which can be detected by measurements along the surface, without considering the space around it.
There is a mathematical way to explain the intrinsic geometric property of a surface that tells when one surface can or cannot be bent into another. The mathematical concept is called the Gaussian curvature of a surface, or often simply the curvature of a surface. This kind of curvature is not to be confused with the curvature of a curve. The curvature of a curve is an extrinsic geometric property, telling how it is bent in the plane, or bent in space. Gaussian curvature is an intrinsic geometric property: it stays the same no matter how a surface is bent, as long as it is not distorted, neither stretched or compressed.
To get a first qualitative idea of how curvature works, here are some examples.
A surface which bulges out in all directions, such as the surface of a sphere, is positively curved. A rough test for positive curvature is that if you take any point on the surface, there is some plane touching the surface at that point so that the surface lies all on one side except at that point. No matter how you (gently) bend the surface, that property remains.
A flat piece of paper, or the surface of a cylinder or cone, has 0 curvature.
A saddle-shaped surface has negative curvature: every plane through a point on the saddle actually cuts the saddle surface in two or more pieces.
Question. What surfaces can you think of that have positive, zero, or negative curvature.
Gaussian curvature is a numerical quantity associated to an area of a surface, very closely related to angle defect. Recall that the angle defect of a polyhedron at a vertex is the angle by which a small neighborhood of a vertex opens up, when it is slit along one of the edges going into the vertex.
The total Gaussian curvature of a region on a surface is the angle by which
its boundary opens up, when laid out in the plane. To actually measure
Gaussian curvature of a region bounded by a curve,
you can cut out a narrow strip on the surface in neighborhood of the
bounding curve. You also need to cut open the curve, so it will be
free to flatten out. Apply it to a flat surface, being careful to
distort it as little as possible. If the surface is positively curved
in the region inside the curve, when you flatten it out, the curve will
open up. The angle between the tangents to the curve at the two sides
of the cut is the total Gaussian curvature. This is like angle defect:
in fact, the total curvature of a region of a polyhedron containing exactly
one vertex is the angle defect at that vertex. You must pay attention
pay attention not just to the angle between the ends of the strip, but
how the strip curled around,
keeping in mind that the standard for zero curvature is
a strip which comes back and meets itself. Pay attention to  's and
's and
 's.
's.
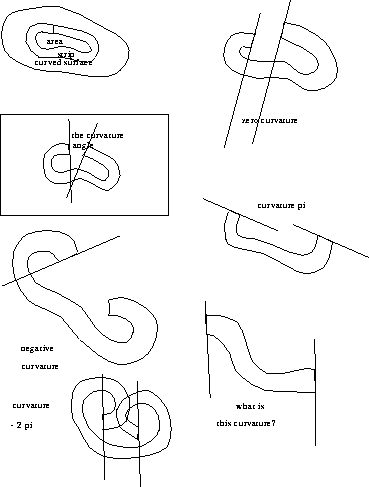
Figure 9: This diagram illustrates how to measure
the total Gaussian curvature of a patch by cutting out a strip
which bounds the patch, and laying it out on a flat surface. The angle
by which the strip `opens up' is the total Gaussian curvature. You must
pay attention not just to the angle between the lines on the paper, but
how it got there, keeping in mind that the standard for zero curvature is
a strip which comes back and meets itself. Pay attention to 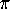 's and
's and
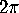 's.
's.
If the total curvature inside the region is negative, the strip will curl around further than necessary to close. The curvature is negative, and is measured by the angle by which the curve overshoots.
A less destructive way to measure total Gaussian curvature of a region is to apply narrow strips of paper to the surface, e.g., masking tape. They can be then be removed and flattened out in the plane to measure the curvature.
Question. Measure the total Gaussian curvature of
The angle defect of a convex polyhedron at one of its vertices can be measured by rolling the polyhedron in a circle around its vertex. Mark one of the edges, and rest it on a sheet of paper. Mark the line on which it contacts the paper. Now roll the polyhedron, keeping the vertex in contact with the paper. When the given edge first touches the paper again, draw another line. The angle between the two lines (in the area where the polyhedron did not touch) is the angle defect. In fact, the area where the polyhedron did touch the paper can be rolled up to form a paper model of a neighborhood of the vertex in question.
A polyhedron can also be rolled in a more general way. Mark some closed path on the surface of the polyhedron, avoiding vertices. Lay the polyhedron on a sheet of paper so that part of the curve is in contact. Mark the position of one of the edges in contact with the paper. now roll the polyhedron, along the curve, until the original face is in contact again, and mark the new position of the same edge. What is the angle between the original position of the line, and the new position of the line?