Exercises in imagining
Next: Curvature of surfaces
Up: Geometry and the Imagination
Previous: Descartes's Formula.
How do you imagine geometric figures in your head? Most people talk about
their three-dimensional imagination as `visualization', but that isn't
exactly right. A visual image is a kind of picture, and it is really
two-dimensional. The image you form in your head is more conceptual
than a picture-you locate things in more of a three-dimensional model than
in a picture. In fact, it is quite hard to go from a mental image to a
two-dimensional visual picture. Children struggle
long and hard to learn to draw because of the real conceptual difficulty
of translating three-dimensional mental images into
two-dimensional images.
Three-dimensional mental images are connected with your visual sense,
but they are also connected with your sense of place and motion.
In forming an image, it often helps to imagine
moving around it, or tracing it out with your hands. The size of an
image is important. Imagine a little half-inch sugarcube in your hand,
a two-foot cubical box, and a ten-foot cubical room that you're inside.
Logically, the three cubes have the same information,
but people often find it easier to manipulate the larger image that they
can move around in.
Geometric imagery is not just something that you are either born with or
you are not. Like any other skill, it develops with practice.
Below are some images to practice with. Some are two-dimensional, some are
three-dimensional. Some are easy, some are hard, but not necessarily in
numerical order. Find another person to work with in going through
these images. Evoke the images by talking about them, not by drawing them.
It will probably help to close your
eyes, although sometimes gestures and drawings in the air will help.
Skip around to try to find exercises that are the right level for you.
When you have gone through these images and are hungry for more,
make some up yourself.
- Picture your first name, and read off the letters
backwards. If you can't see your whole name at once,
do it by groups of three letters. Try
the same for your partner's name, and for a few other words.
Make sure to do it by sight, not by sound.
-
Cut off each corner of a square, as far as the midpoints of the edges.
What shape is left over? How can you re-assemble the four corners to make
another square?
-
Mark the sides of an equilateral triangle into thirds. Cut off each corner
of the triangle, as far as the marks. What do you get?
-
Take two squares. Place the second square centered over the first square
but at a forty-five degree angle. What is the intersection of the two
squares?
-
Mark the sides of a square into thirds, and cut off each of its corners
back to the marks. What does it look like?
-
How many edges does a cube have?
-
Take a wire frame which forms the edges of a cube. Trace out
a closed path which goes exactly once through each corner.
-
Take a
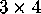 rectangular array of dots in the plane,
and connect the dots vertically and horizontally. How many squares
are enclosed?
rectangular array of dots in the plane,
and connect the dots vertically and horizontally. How many squares
are enclosed?
-
Find a closed
path along the edges of the diagram above which visits each
vertex exactly once? Can you do it for a
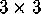 array of dots?
array of dots?
-
How many different colors are required to color the faces of a cube so that
no two adjacent faces have the same color?
-
A tetrahedron is a pyramid with a triangular base. How many faces
does it have? How many edges? How many vertices?
-
Rest a tetrahedron on its base, and cut it halfway up. What shape is the
smaller piece? What shapes are the faces of the larger pieces?
- Rest a tetrahedron so that it is balanced on one edge,
and slice it horizontally halfway between its lowest edge and its highest
edge. What shape is the slice?
-
Cut off the corners of an equilateral triangle as far as the midpoints of its
edges. What is left over?
-
Cut off the corners of a tetrahedron as far as the midpoints of the edges.
What shape is left over?
-
You see the silhouette of a cube, viewed from the corner. What does
it look like?
-
How many colors are required to color the faces of an octahedron so that
faces which share an edge have different colors?
-
Imagine a wire is shaped to go up one inch, right one inch, back one inch,
up one inch, right one inch, back one inch, .... What does it look
like, viewed from different perspectives?
- The game of tetris has pieces whose shapes are all the
possible ways that four squares can be glued together along edges.
Left-handed and right-handed forms are distinguished. What are the shapes,
and how many are there?
- Someone is designing a three-dimensional tetris, and wants
to use all possible shapes formed by gluing four cubes together. What
are the shapes, and how many are there?
- An octahedron is the shape formed by gluing together
equilateral triangles four to a vertex. Balance it on a corner, and
slice it halfway up. What shape is the slice?
- Rest an octahedron on a face, so that another face is
on top. Slice it halfway up. What shape is the slice?
- Take a
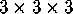 array of dots in space,
and connect them by edges up-and-down, left-and-right, and forward-and-back.
Can you find a closed path which visits every dot but one exactly once?
Every dot?
array of dots in space,
and connect them by edges up-and-down, left-and-right, and forward-and-back.
Can you find a closed path which visits every dot but one exactly once?
Every dot?
- Do the same for a
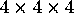 array of dots,
finding a closed path that visits every dot exactly once.
array of dots,
finding a closed path that visits every dot exactly once.
-
What three-dimensional solid has circular profile viewed from above,
a square profile viewed from the front, and a triangular profile viewed
from the side? Do these three profiles determine the three-dimensional
shape?
-
Find a path through edges of the dodecahedron which visits each vertex
exactly once.
Next: Curvature of surfaces
Up: Geometry and the Imagination
Previous: Descartes's Formula.
Peter Doyle
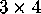 rectangular array of dots in the plane,
and connect the dots vertically and horizontally. How many squares
are enclosed?
rectangular array of dots in the plane,
and connect the dots vertically and horizontally. How many squares
are enclosed?
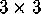 array of dots?
array of dots?
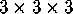 array of dots in space,
and connect them by edges up-and-down, left-and-right, and forward-and-back.
Can you find a closed path which visits every dot but one exactly once?
Every dot?
array of dots in space,
and connect them by edges up-and-down, left-and-right, and forward-and-back.
Can you find a closed path which visits every dot but one exactly once?
Every dot?
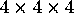 array of dots,
finding a closed path that visits every dot exactly once.
array of dots,
finding a closed path that visits every dot exactly once.