 Teichmuller Navigator 2.0
Teichmuller Navigator 2.0 Teichmuller Navigator 2.0
Teichmuller Navigator 2.0An undergraduate research project by Deva Van Der Werf, at the Geometry Center Summer Institute 1993. Mentors: Paul Burchard, David Ben-Zvi, Oliver Goodman. World Wide Web front end by Paul Burchard and Daeron Meyer.
Teichmuller Navigator is an interactive introduction to the geometry of Teichmuller Space. You can read Deva's report to find out what Teichmuller space is, and how the program helps to navigate it. There is also a brief explanation below.
But if you want to start by trying out the program, then just click near the blue points in the navigator, and see what happens!
Consider a two-holed torus with an angle geometry on it (this is called a Riemann surface of genus 2). As shown in the picture below, it is possible create a flat octagonal "map" of the surface by cutting it open along some curves, and then reassembling it. The map can even be made to correctly depict the angles on the surface (a map like this is called conformal).

Since the angles at the vertices of this octagon add up to only 360 degrees, the sides cannot be straight lines in Euclidean geometry. But it is possible to make the sides be "straight" in hyperbolic geometry, a kind of space in which parallel lines tend to diverge from one another (see the Geometry Forum article on hyperbolic geometry for background information). Because the sides of the map are straight in hyperbolic geometry, we can glue together the edges of different copies of the map, in such a way that continuous travel on the surface doesn't make you "fall off the map", but merely causes you to travel from one copy of the map to the next one.
Teichmuller Navigator uses this tiled, conformal map of the surface in the hyperbolic plane as a substitute for the original surface with its angle geometry. Putting the surfaces into this standardized format allows us to "navigate" through the space of all such surfaces, by simply changing the shape of the octagonal tile. In the interactive navigator, you can change the tiling by clicking near one of the blue points, to indicate where you would like it moved.
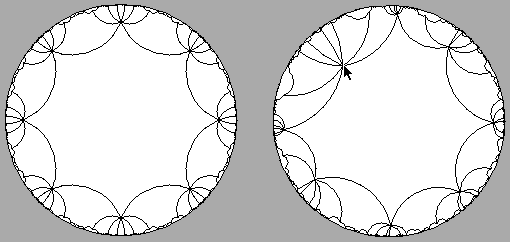
However -- not all octagonal tiles fit together properly to create the map of a surface! Notice that in the picture above, all of the vertices of the central octagon have been moved a bit; this was necessary to make the different copies of the octagon fit together without gaps or overlaps. What Teichmuller Navigator does is to take the tile shape you request, and find the hyperbolically closest tileable octagon which has one vertex at the requested location. This is the program's main computation.
Conversely, it is also true that different octagon shapes can produce maps of the same surface. This can happen, for example, if the same surface is cut open at different points. Teichmuller Navigator does not indicate this redundancy.
The Geometry Center University of Minnesota 400 Lind Hall 207 Church Street S.E. Minneapolis, MN 55455