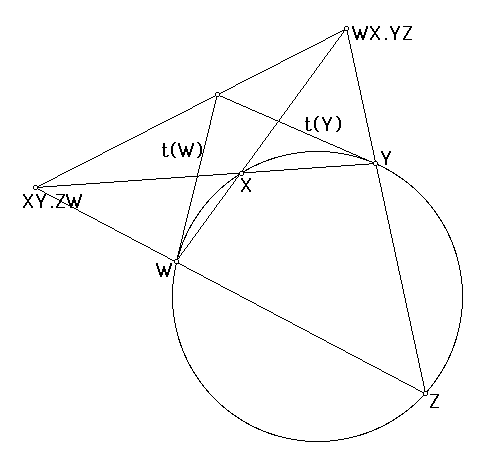

Theorem: Any point conic also arises as a line conic.
Proof: We select four points on our conic: A, B, C, and D, and take tangents to all of them: T(A), T(B), T(C), and T(D). Then we define:
B1=T(A).T(B); C1=T(A).T(C); D1=T(A).T(D);
A2=T(B).T(A); C2=T(B).T(C); D2=T(B).T(D).
Now A, B1, C1, and D1 all lie on T(A), as A2, B, C2, and D2 all lie on T(B). Note also that A2 is the same point as B1, and lies on both T(A) and T(B).
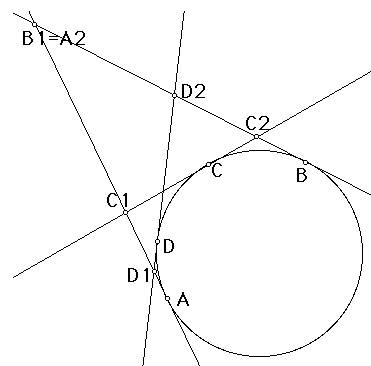
We need to prove that (A,B1;C1,D1) = (A2,B;C2,D2). When we have this, we can fix a projectivity from T(A1) to T(B2) by A->A2, B1->B, C1->C2. Then given any other point D on the conic, we can see that its tangent was a constituent of the line conic because this projectivity took D1 to D2--i.e. (A,B1;C1,D1) = (A2,B;C2,D2).
Proof of equality of cross ratios: Set up the diagonal triangle for A, B, C, D; let P=AD.BC, Q=AC.BD, and R=AB.CD. Then the above theorem tells us that A2=B1 lies on PQ; C1 and D2 lie on PR; C2 and D1 lie on QR. Now we set up a projectivity through R, and find that (A,B1;C1,D1) = (B,A2;D2,C2). Since we also know that (B,A2;D2,C2) = (A2,B;C2,D2), we indeed have the desired result: (A,B1;C1,D1) = (A2,B;C2,D2).
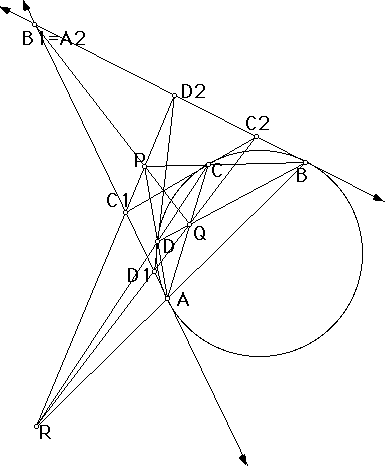
The converse of this theorem is its dual. We could prove it using the duals of all the results in this proof; in particular, we would begin with a special case of Brianchon's theorem in which a quadrilateral is circumscribed to a conic.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: Nov 30 1995 ---
Last modified: Thu Nov 30 15:25:18 1995