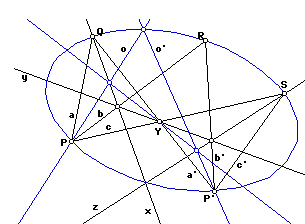
Let a, b, c be lines from P to Q, R, S. Let a', b', c' be lines from P' to Q, R, S.
Let y be a line on the point Y=a'.c.
Let x be the line (a.a')(b.y).
Let z be the line (y.b')(c.c').
Now, given any line o on P, use x to project it onto the point Y. Then use z to project this new line onto the point P', and call the result of this projection line o'. Our conic is the locus of intersections of o and o', as o becomes each line on the point P.
In order to construct our conic, we needed to construct a projectivity that sent a=PQ to a'=P'Q, b=PR to b'=P'R, and c=PS to c'=P'S. Because there is only one such projectivity, any construction giving those three correspondences will yield the same projectivity. In particular, this shows that our conic did not depend on our choice of line y. Our choice of line did affect the particulars of our construction, but it did not affect the projectivity or the conic.
This construction, like all constructions in projective geometry, requires a straightedge only. Nonetheless, if you use this graphic in Geometer's Sketchpad and show all hidden objects, you may see a circle. This is just a convenient way of generating the set of all lines lying on a point; alternatively (although it would not work so well in Geometer's Sketchpad), we could take the locus of lines going through that point and the points of some other line.
![[HOME]](/pix/home.gif) The Geometry Center Home Page
The Geometry Center Home Page
Comments to:
webmaster@www.geom.uiuc.edu
Created: Nov 30 1995 ---
Last modified: Thu Nov 30 15:32:07 1995