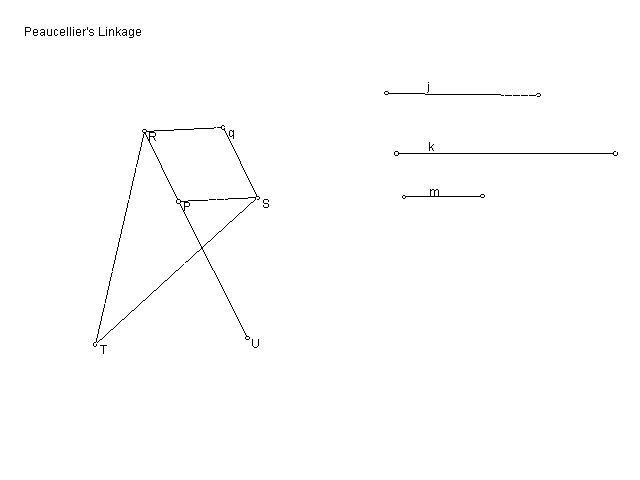
This is a link to Tom's web page
This is a link to Kristine's web page
1. Here is the picture and sketch of Peaucellier's linkage.
2. This script constructs the inverse of a point with respect to a circle.
3. Inversion Equation AF' = ((AR)/AF)) (AR)
3.1 A point inside a circle of inversion has an inverse outside the circle. (AR / AF ) > 0
3.2 A point outside a circle of inversion has an inverse inside the circle. (AR / AF ) < 0
3.3 All the points on a circle of inversion are their own inverses. AR = AF = AR
3.4 The inverse of the center of a circle of inversion is undefined. As a point approaches the center of the circle of inversion, the inverse of the point approaches infinity.
4.
| Shape inverted | Inverse of shape |
| Circle through A | a line |
| Circle not through A | circle outside the circle of inversion |
| Line through A | a line |
| Line not through A | a circle |
5. First we constructed the circle of inversion and the circle to be inverted. The circle to be inverted was constructed to go through the center of the circle of inversion. We know that the inverse of a circle through the center of the circle of inversion is a line. So we found the inverses of two random points on the circle to be inverted using a previous script and constructed the inverse line through them.

6. Again we constructed the circle of inversion and the line not through its center. We know that the inverse of such a line is a circle. Thus we selected three random points on the line and found their inverses. Then we constructed the inverse circle through these points by finding the intersection of perpendicular bisectors.

7. As point P travels a circluar path centered at U and through T, Point Q travels in a straight line. We know from our chart that this is the case of a circle that passes through the center of Ci being inverted. For any point P on its circle, P, Q, and T are collinear. So P and Q are related by inversion an d T must be the center of the circle of inversion.
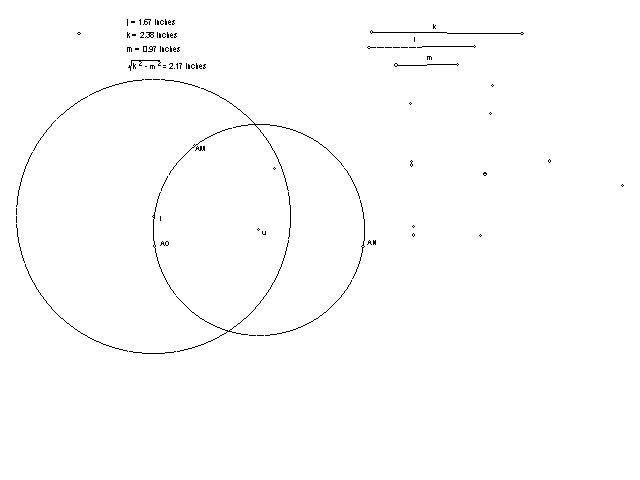
8. The radius of the circle of inversion is K^2-M^2. This length can be constructed: draw a line, draw a point on the line, mark a distance m on either side of the point on the line, from each of these points draw a circle of radius k, the radius of the inversion circle is the distance from the circle intersections to the original point on the line.
The sketchpad script below will construct the radius of an inversion circle for any two segments.
This sketch pad drawing shows the linkage and the circle of inversion.
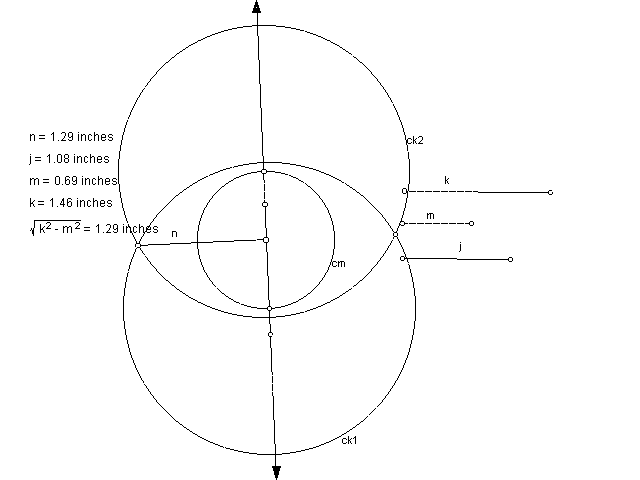
9. This sketch pad sketch shows q as the inverse of p using inversion. We used the original 3 segment lengths. Then, we constructed the the circle of inversion using our script from problem 8. A circle of radius J, through the center of the inversion circle was constructed. Three random points on the circle J were selected and inverted using the script from problem 2. The inversion points were then connected with a line.