1. From part 1: How do you construct a tangent line to a circle through a point not on a circle?
Steps:
- make a circle, center O
- select point, Q, somewhere outside circle
- draw segment, OQ
- find midpoint of segment OQ. point M
- draw circle, center M
- circle m intersects circle O at points P and N, circle M goes through both O and Q
- draw line NQ and PQ
- hide line segment OQ and circle M
Math Fact: - If given circle O and line segment OQ, the circle formed at the midpoint of OQ and having diameter OQ will intersect circle O at tangents from point Q.
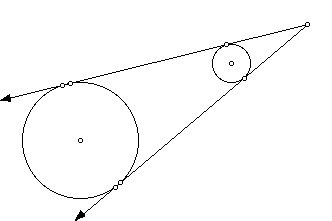
2. From part 2: How do you construct an external tangent to two circles?
Steps:
- make circles O1 and O2
- select point Q on circle O1
- construct line m connecting points O1 and Q
- construct line n that is parallel to line m passing through point O2
- make point R at intersection of circle O2 and line n
- construct line s connecting points O1 and O2
- construct line t connecting points Q and R
- construct point P where lines s and t intersect
- construct segment between O2 and P
- find midpoint of segment O2P, labeled M
- make circle M, centered at M with diameter O2P
- construct points W and X at intersections of circle M and circle O2
- construct ray PW
- construct ray PX
- construct points Y and Z at intersection of rays and circles O1
Thus, rays PW extends to PY and is an external tangent to two circles O1 and O2. And, rays PX extends to PZ and is an external tangent to two circles O1 and O2. Hide all unwanted objects.
Math Fact:
- The same math fact is used as in part 1 - the midpoint of a segment is used to find a tangent given a point and a circle. In this case we use the fact that we are using parallel lines and thus can find an external tangent to two circles.

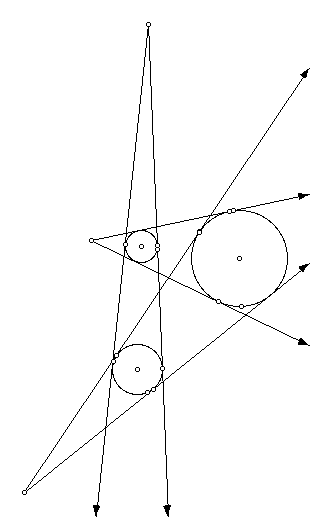
3. From part 3: State Monge's Theorem
To construct Monge's theorem use the script/steps used for part 2, repeat twice using on each pair of circles. The three points connecting the tangent lines for each pair of circles, are collinear. (i.e. P1, P2, P3 are collinear)
The circles can be dragged around using the pointer. Points P1, P2, and P3 continue to be collinear. Cool!!
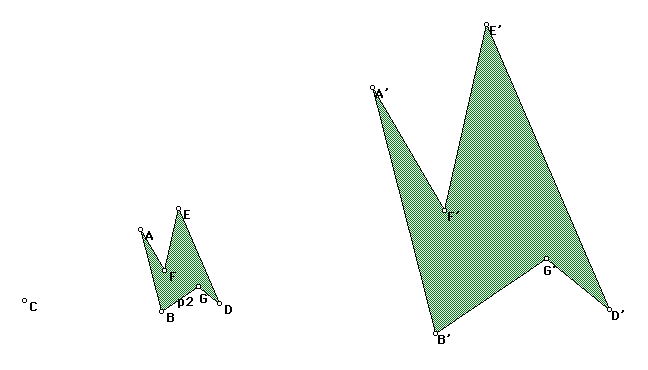
4. From part 4: Dilation
Given two points A and A', does there exist a dilation such that A' is the image of A under dilation?
In order to have A' be an image of A under a dilation, a center of dilation, C, must be present. If a center is given, then the dilation factor can be found for A and its image A'. Because only two points are given, one could work backwards to make a center of dilation and then find the scale factor. Otherwise, I wouldn't consider just two points to be part of a dilation.
Given four points A, A', B, and B', does there exist a dilation such that A' is the image of A and B' is the image of B?
Because there are four points given, each pair can represent a line. There will be a specific center of dilation, C, where these represented lines cross. Thus, with this center of dilation, a dilation scale factor can be found.
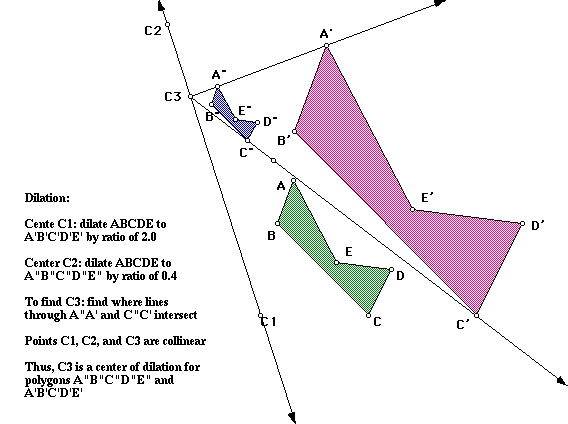
5. Why are three centers of dilation collinear when one makes a composition of two dilations?
This will only work when the product of the ratios of dilation is not equal to 1. If the product is 1, then the figure is translated, and there will be no common center of dilation. If the product of the ratios is 1, then the lines connecting corresponding points are parallel, and thus will never intersect to form a third center of dilation.
When are two circles related by a dilation?
Dilation will work for circles. The center of dilation for circles is the point at which the tangent lines for the two circles meet. The line connecting the centers of the circles will pass through this center also, just as it is a point to be dilated by the ratio.
Justify Monge's Theorem:
I can see the similarities between the finding of a third center of dilation that is collinear to the previous two centers when making a composition of two dilations, and with Monges Theorem activity that finds the external tangents for each pair of a set of three circles. In fact, thats exactly what dilation does to a set of two circles; a center gives two tangent lines to each pair of circles. In both cases the centers, or points of tangent intersection are collinear.
6. Web page http://www.geom.umn.edu/~banchoff/mongepappus/MP.html. New mathematical idea.
This web page explains many of the same concepts that we just developed while completing the Monge lab. It explains that the external tangents to three circles will form intersection points that are collinear. The web page then suggested that this is just showing three points of dilation on three circles. What I found to be interesting was the continuation of this idea when four spheres were used instead of circles. The four spheres then have six pairs, forming six points of intersection, these six points are coplaner. I enjoyed seeing a concept that was found by our group through guided discovery in a lab assignment, used and developed in a third dimension.
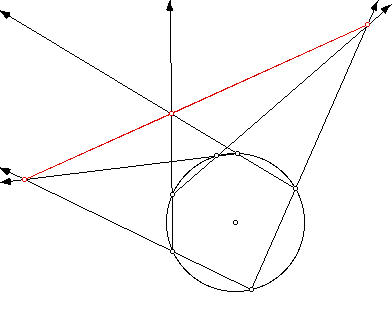
7. Use the picture of the hexagon inscribed in a circle in our packet. Does this remind one of Monge's Theorem?
This sketch does remind me of Monge's theorm simply because there are three intersection points shown and they seem to be collinear. I have had trouble making a similar sketch on Geometer's Sketchpad, that works. Basically, what I see happening is three pairs of chords (of the hexagon) are extended. With each pair, the other vetex of the hexagon (the one not included in the pair) is found in the internal angle of the intersecting pair.
Below is a picture of this sketch where the intersections of non-consecutive sides of an inscribed hexagon in a circle. The intersection points are collinear.
8. Making the tangent to a circle with a straight-edge and compass.
Step 1: Start by drawing a circle with your compass. Label the center A and the circle C1.
Step 2: Pick any point outside the circle. Label it Q.
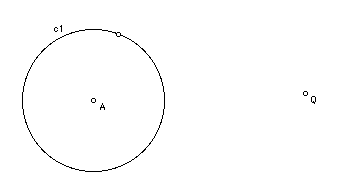
Step 3: Using the straight edge, connect the center of the circle, point A, with the point outside the circle, Q.
Step 4: Find the midpoint of segment AQ. In order to find the midpoint we will construct the perpendicular bisector of AQ. If you have forgotten how to do this, use these tips. Set compass at some set width. Sweep two arcs, using both A and Q for centers. Construct the line connecting the two points where these arcs intersect. This is the perpendicular bisector. Label the point where it intersects segment AQ, M. Point M is the midpoint of AQ.
Step 5: Now make another circle. This time make point M the center of the circle. Set the compass at the width of the distance from M the Q. Draw the circle. Label it circle C2. The circle should go through both Q and A. Remember, the center is at M.
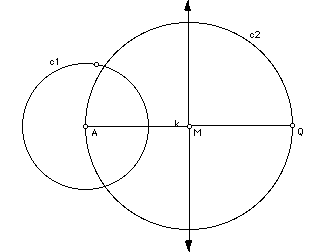
Step 6: Now, label the points of intersection between circles C1 and C2. Label them X and Y.
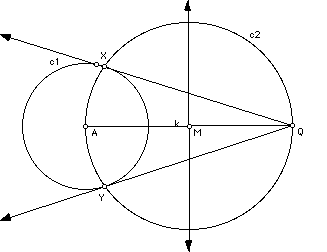
Step 7: Using your straight edge, draw a line connecting point X to point Q. Draw another line connecting point Y to point Q. These lines are the tangent lines to circle C1 to point Q.
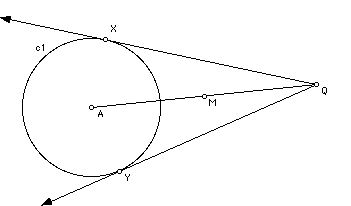
You now have constructed the tangent lines to a circle!!