
(High school/college level)
The formulas y=k x^2 and y=k cosh(x/k) for the shape of the cables come from considering all of the forces acting on the cable at any given point. We won't derive the formulas here, because they involve solving differential equations. But it's fun to figure out what the forces are anyway.
Let P be some point on a freely hanging cable. You can imagine that if we knew what the angle a between the cable and the horizontal was at every such point P, then we could draw the curve exactly.

So that's what we're going to do: describe what the angle a is at every point.
Let's focus on P. The forces in the rope at P are tangent to the rope: there is a force T pulling up and to the right, which is balanced by a force U pulling down and to the left.
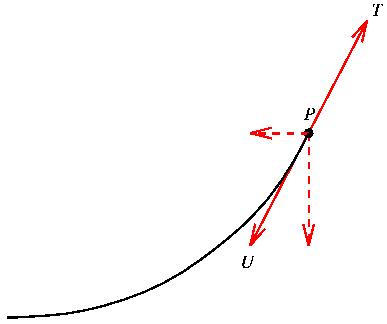
We will concentrate on the force U. We can break U into its horizontal (left) and vertical (down) components, as pictured above. The force pulling down is the force due to gravity -- in other words, the force due to the weight of the part of the cable pulling down on P. But which part? Certainly the portion of the rope above and to the right of P isn't pulling at P. What about the portion to the left?
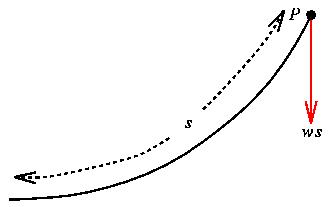
If you think about it, you can convince yourself that it's only the portion of the cable from P to the lowest point that is pulling down at P. If you have a piece of heavy rope, you can experiment by hanging it between your hands. As you raise your left hand, you can feel the weight supported by your right hand decreasing. At the lowest point, the rope is horizontal, which means that all forces are pulling to the left and right, and there is no downward component.
So, if w equals the the weight of the rope per unit length, and we let s be the length of the portion of the rope between the lowest point and P, then P feels a force of ws pointing straight down.
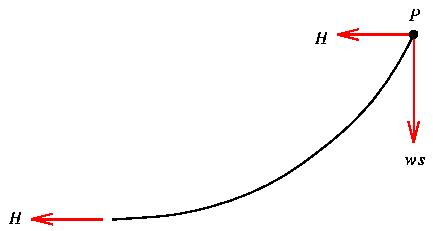
Now what about the force pulling to the left? The only horizontal force anywhere on the rope is the tension due to stretching the rope between the pylons. Since this is the only horizontal force, and since the rope is in static equilibrium, every point on the rope feels the same horizontal tension H. We could measure H at the lowest point, where there are no other forces acting.
So the force vector U has horizontal component H and vertical component ws. These must match the horizontal and vertical components of T.
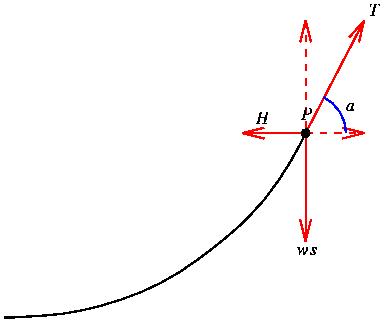
In terms of the angle a we have

Notice the tension T in the suspension cables increases as s increases. The tension is maximum at the top of the pylons, where the cable is supported.
The two equations imply that
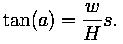
We've done it. This equation describes the angle of the curve at each point, as a function of the distance s from the lowest point. Both w and H are constants. The constant w is just a property of the cable, and the tension H at the lowest point is something we can control -- as we take up the slack in the cable, H increases.
Exercise 1: Use what you know about the tangent function to describe how a changes when we change w and H. For example, if the weight per unit length w is fixed, and the tension H is increased, how does a change at a fixed distance s along the cable? Describe how this changes the shape of the catenary.
The quantity tan(a) is telling us the slope of the tangent line to the cable at each point. This is a concept central to calculus, and knowing some calculus would enable us to use the above equation for tan(a) to see that the equation of the curve described by the cable is
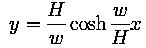 .
.
What changes when we hang a heavy road from our suspension cable? Not much, really! The only thing that changes in the above discussion is the weight pulling down at the point P. We will assume that the weight W per unit length of road is much heavier than the weight w per unit length of cable. In that case, the weight supported at P is essentially Wx, where x is the horizontal distance from the lowest point, instead of the distance s along the cable.
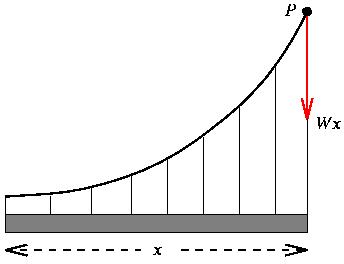 .
.
Exercise 2: Use this to show that the equation for a becomes
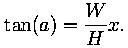
Thus the equation describing a is a function of x instead of s. It leads to the equation
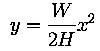
for the cable supporting a heavy road.