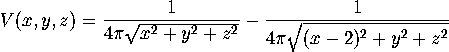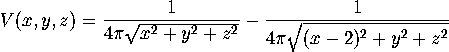3D Flux through a Plane

Although an electric field does not contain fluid, it is useful to use the concept of flux to describe the "amount" of electric field that passes through a surface. Loosely speaking, the electric flux determines the intensity of the electric field on a surface.

Again, picture a positive unit of charge at the origin and a negative unit of charge at (x,y,z)=(2,0,0). The full 3D electric potential generated by these charges is proportional to

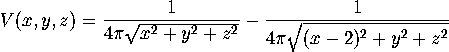
In Maple we can define the electric potential and field by

  V:= 1/(4*Pi*sqrt(x^2+y^2+z^2)) - 1/(4*Pi*sqrt((x-2)^2+y^2+z^2));
  EField:= grad( -V, [x,y,z] );

In the following exercise, you will determine the electric flux through the (infinite) plane defined by x=1. We will follow the same steps we followed in class.

Question #2

1. Define g to be a (vector-valued) expression in s,t that parametrizes the plane defined by x=1. Hint: if g is the Maple expression that defines the parametrization, then plotting
   plot3d( g, s=-1..1, t=-1..1 );
   should give you a portion of the plane x=1.)
2. To find the electric field at an arbitrary point on the plane, substitute your parametrization into your expression for the electric field. For example
   F:= subs(x=g[1],y=g[2],z=g[3], eval(EField));
   will probably work.
3. Let n be the unit normal to the plane. Since there are two normals that you could choose, let's all choose the one that points towards large values of x.
4. Define A to be the expression that gives the area of the parallelogram formed by tangent vectors to the parametrized plane. Hint: Although in general this expression will be a complicated function of the two parameters, A will probably be very simple for your parametrization of the plane.
5. The total flux across the surface is a double integral. In terms of what we've done so far, the quantity to integrate is
   integrand:= innerprod(F,n)*A;
6. If we integrate this quantity over the plane, we get the total flux. To aid in visualizing what is happening:
   • Integrate the integrand over the square defined by x=1, -L < y < L, and -L < z < L. You may be able to simplify the resulting expression more than Maple can!
   • Plot this expression for 0 < L < 100. Describe what the plot tells us about the flux through the plane
     • near the x-axis
     • far away from the x-axis
   • Take the limit as L increases to infinity in order to determine the flux through the infinite plane. Hint: The total flux should be a very simple expression!