Divergence at a Point
In this lab we will consider the vector field given by the equations:
dx/dt = y
dy/dt = -x^3 + x + (3/2)x^2 + y - x^2 y
The phase portrait of this vector field looks like Figure 1. (Follow
this link to
enter this dynamical system and plot more trajectories -- you will
need a Java-enhanced browser).
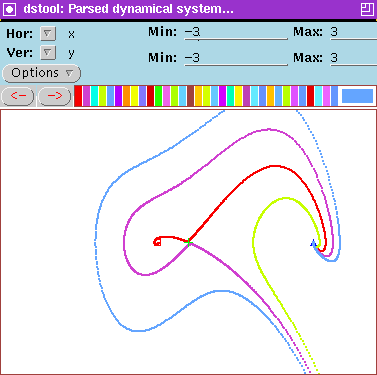
Figure 1: Phase portrait and equilibria.
Let f denote the right-hand side of this system,
f(x,y)=(y, -x^3 + x + (3/2)x^2 + y - x^2 y),
and recall that
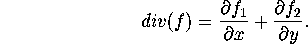 .
.
Question #1
- Compute the location of equilibria for this vector field.
- Compute div(f).
- Evaluate div(f) at each equilibrium.
- Based on the previous computation, what do you think is the stability
type of each equilibrium? How confident are you?
Next: Divergence over a Region
Previous: Introduction
Robert E. Thurman <thurman@geom.umn.edu>
Document Created: Wed Jan 25 CST
Last modified: Thu Mar 27 15:09:19 1997
 .
.
 .
.