Torus Knots

For this lab, you will want to load some standard Maple packages:

with(plots): with(linalg):

Recall that a torus may be parametrized by rotating a circle of radius r about another circle of radius R. For concreteness, let r=1 and R=2. Then a parametrization of the torus may be written:

T(s,t) = ( (2+cos(t))cos(s), (2+cos(t))sin(s), sin(t) )

In Maple, such a function would be written as

T:=(s,t)-> [(2+cos(t))*cos(s),(2+cos(t))*sin(s),sin(t)];

Note that the image of T is in R^3 whereas the domain of T is in the plane.

A torus knot is a closed curve that winds around the torus. You can generate torus knots by specifying an integer relationship between the parameters s and t. For example, if we restrict T to the curve t=2s, then we get a parametrized curve
T(s,2s) = ( (2+cos(2s))cos(s), (2+cos(2s))sin(s), sin(2s) )

This curve wraps around the torus once in the "long" direction while it wraps around the torus two times in the "short" direction, as indicted in Figure 1.

Figure 1. The mapping that takes the curve t=2s to the torus knot of type (1,2).

Activity #1

Use the Maple command

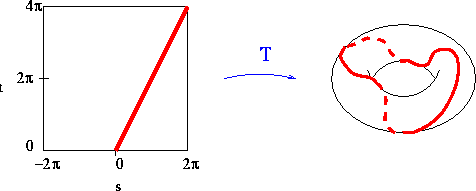
spacecurve(T(s, 2*s), s=0..2*Pi);

to plot the torus knot. You can try to display this along with a plot of the torus,

plot3d(T(s,t),s=0..2*Pi,t=0..2*Pi);

but the results are not very satisfying.

In general, for nonzero integers m,n, a torus knot of type (m,n) is the image of the line ns=mt + const. (The constant moves the knot around, but doesn't change the way that it winds.) This image will wind around the torus m times in one direction and n times in the other direction. If either m=0 or n=0, then the definition changes slightly: a torus knot of type (1,0) is the image of the line t=constant whereas a knot of type (0,1) is the image of a line s=constant.

Question #1

For each of the torus knots below, imitate Figure 1 to sketch a line in "parameter space" (the domain of T) and the image under T of that line on the torus. When a point is given, indicate that point and its image on the sketch. Hint: First express the curve in (s,t) space as a graph (s, t(s)), then look at the image of this curve under T. You may want to print out a plot of the torus alone and sketch the knot on it.
Next: Building a Surface from Torus Knots
Previous: Introduction
Robert E. Thurman<thurman@geom.umn.edu>
Original lab created by Frederick J. Wicklin

Document Created: Thu Feb 23 1995
Last modified: Mon Mar 10 16:56:20 1997