Brianchon's Theorem
Another way of stating Pascal's theorem is: If points
ABCDEF lie on a conic, then points AB.DE, BC.EF, and CD.FA
lie on one line. This shows the way to a dual theorem,
known as Brianchon's theorem: if lines abcdef lie on a
conic, then lines (a.b)(d.e), (b.c)(e.f), (c.d)(f.a) lie
on one point. If six lines lie on a conic, then the
hexagon which they form circumscribes the conic. So
the more traditional form of Brianchon's theorem is:
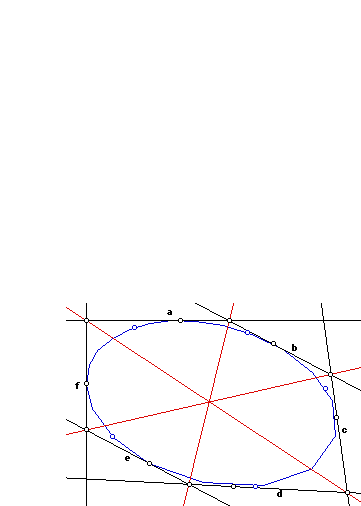
If a hexagon is circumscribed about a conic, its diagonals
are coincident.
Brianchon's theorem has a converse, too:
If the diagonals of a hexagon are coincident, then the
hexagon may be circumscribed about a conic.
The proofs for these are exactly the duals of the proofs
for Pascal's theorem and its converse.