Up to Pisces Online Documentation

Recursive Surface Algorithm

( also known as "RSurf" )

Overview

This algorithm approximates the zero level set of a function of three variables. That is, given a function from R^3->R, this algorithm computes the level set of zero associated to that function.

How Recursive Surface Works

The basic step of RSurf is to subdivide a cube into eight smaller cubes. The initial cube is the bounding domain. The algorithm starts by replacing the initial cube and all that result until all the cubes have some minimum required depth. A cube's depth is the depth it has in the octree that results from the cube replacement. The algorithm continues by subdividing when a cube has not reached the maximum allowed depth and, the eight numbers that result when you evaluated the function at the vertices of the cube do not have the same sign.

Once a cube has reached its maximum depth, a polygonal approximation to the surface is made by:

Start at the first edge with a sign crossing.
Look up which edges can be next based on what the current edge is and its orientation.
Decide which of these three edges have the sign crossing.
Continue until back to the first edge.
The polygon is then made up of the traversed edges crossings.

The algorithm is currently implemented recursively.

Controlling the algorithm from Pisces

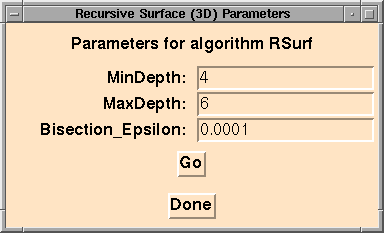
The Pisces panel to the RSurf algorithm has 3 parameters:

MinDepth: All cubes are divided until they have at least minimum depth.
Example: If MinDepth is 3, then the original cube (the bounding domain) is divided into 8 cubes, each of the 8 into 8 cubes, and each of the resulting 64 into 8 cubes resulting in 512 cubes filling the original bounding domain.
Default Value: 4
MaxDepth: No cubes are allowed to have depth greater than the maximum depth.
Example: If the MaxDepth is 5, then if a cube has depth 5 it will not be subdivided any further, but rather a polygonal approximation to the surface will result instead.
Default Value: 6
Bisection_Epsilon: When bisecting the edge of a cube to find out where the surface crosses the edge, the bisection process stops on an interval of Bisection_Epsilon.
Default Value: 0.0001

Known Bugs

A memory allocation error will cause Pisces to crash. This is currently being looked at.

Bug Reports

software@geom.umn.edu

Algorithm Implemented by

Daniel B. Krech

Acknowledgements

The algorithm was inspired after working on implementing a brute force method for finding curves in the plane. The method involved dividing each "scan line" up into n segments, doing bisection on any segment where the functions sign changed and drawing the pixel that results from the bisection.

The Pisces Home Page

The Geometry Center Home Page

Comments to: pisces@geom.umn.edu
Created Mon May 15 10:00:03 CDT 1995 by Dan Krech
Converted to html on July 26, 1995 by Erik Streed
Last Modified: July 26, 1995
Copyright © 1995 by The Geometry Center, all rights reserved.