Click on the sketch to view the construction.

Peaucellier's Linkage Question 2

The following is an example construction of the inverse of a point in a circle.

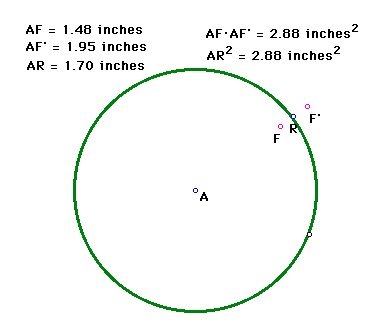
Click on the sketch to access the script of this construction.

Peaucellier's Linkage Question 3

• Where is the inverse of a point inside the circle?

  Outside the circle at a distance equal to the radius squared divided by the distance from the center to the point.

• Where is the inverse of a point outside the circle?

  Inside the circle at a distance equal to the radius squared divided by the distance from the center to the point.

• Are there points that are their own inverses?

  Yes. All points contained on the circle because the ratio at these points is one.

• Where is the inverse of the center of the circle?

  The inverse of the center of the circle does not exist since the distance from the center of the circle to the point is zero, hence the ratio is undefined.

Peaucellier's Linkage Question 4

Circle through A: line

Circle not through A: circle

Line through A: line

Line not through A: circle

To see this happen you can access our sketch. Select point F and any circle or line and choose ANIMATE from the DISPLAY menu option. Have fun.

Peaucellier's Linkage Question 5

• Construct circle c1 with center A.
• Construct a second point B (not point A).
• Select points A and B and construct a circle (c2) centered at B through A.
• Construct point F on circle c2.
• Construct a ray originating at A passing through F.
• Construct point R where the ray crosses c1.
• Construct segment AF.
• Construct a second segment from A to any point on c1 (it will make it easier if you do not choose R as your point on c1). We will call this the radius segment.
• Select the radius segment and then the segment AF (using the shift key) and mark the ratio.
• Mark A as center.
• Dilate R by the marked ratio.
• Name the dilation of R, F'.

This point F' can be used to trace the line that is the inverse of a circle c2.

To run a script of this construction click on the sketch.

Peaucellier's Linkage Question 6

• Construct circle c1 with center A.
• Construct line j not passing through A.
• Construct point F on j.
• Construct a ray originating at A passing through F.
• Construct point R where the ray crosses c1.
• Construct segment AF.
• Construct a second segment from A to any point on c1 (it will make it easier if you do not choose R as your point on c1). We will call this the radius segment.
• Select the radius segment and then the segment AF (using the shift key) and mark the ratio.
• Mark A as center.
• Dilate R by the marked ratio.
• Name the dilation of R, F'.

This point F' can be used to trace the circle that is the inverse of a line j.

To run a script of this construction click on the sketch.

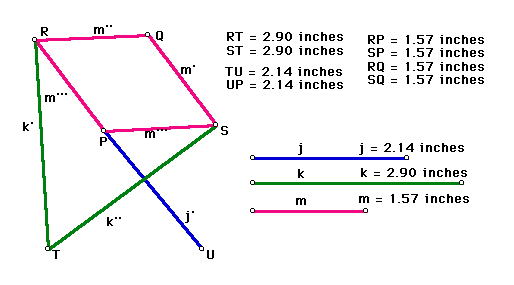
Peaucellier's Linkage Question 7

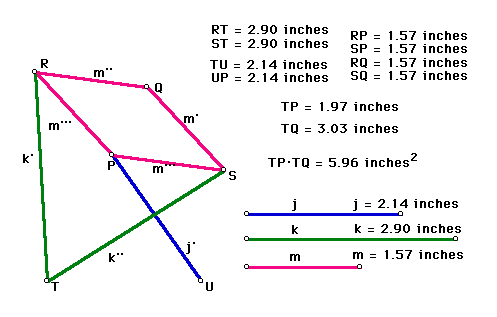
To verify that P and Q are related by inversion we measured the distance from T to P and multiplied it by the distance from T to Q. We found this to be 5.96 square inches. When P is moved around the construction we can see that the calculation 5.96 does not change. By constructing a line through P and Q we see that T lies on the same line, thus P, Q, and T are collinear. This indicates that T is the center of inversion. Therefore, by the definition of inversion, P and Q are related by inversion.

Peaucellier's Linkage Question 8

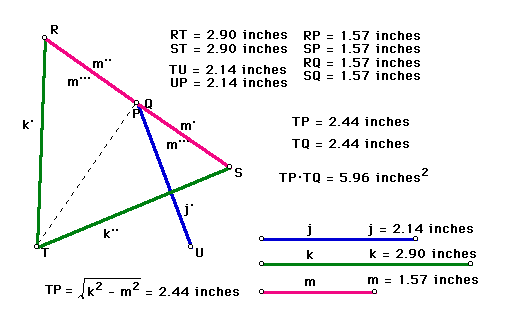
To determine the radius of the circle of inversion we first moved point P until it the construction showed points P and Q to be the same point. The only time that P and Q can be the same point is if P lies on the circle of inversion, therefore, the length of the line connecting points T and P is the radius of the circle of inversion. By constructing this line (see the dashed line in the above sketch), we formed a right triangle with one leg of length m and the hypotonuse of length k. By using the Pythagorean Theorem we determined that the length TP, and thus the radius of the circle of inversion, is equal to the square root of the quantity k squared minus m squared.

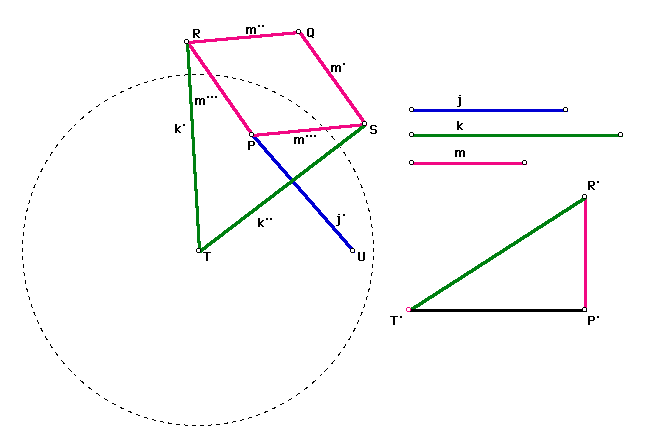
Constructing a segment of the length of the radius using the segments of length j, k, and m:

• Construct a horizontal line.
• Construct a point anywhere on the horizontal line. Name this point P'.
• Select the point and the horizontal line and construct a perpendicular line.
• Select P' and the line m and construct a circle by center and radius.
• Construct a point at the intersection of the circle and the vertical line. Name this point R'. Hide the circle.
• Select R' and the line k and construct a circle by center and radius.
• Construct a point at the intersection of the circle and the horizontal line. Name this point T'. Hide the circle.
• Select points T' and P' and construct a line segment. This line segment is the length of the radius.

By selecting point P and the segment T'P' you can construct the circle of inversion by constructing a circle by center and radius.

Peaucellier's Linkage Question 9

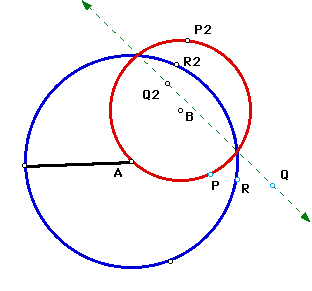
Click on the sketch to move point P and view the actual trace of point Q.