Constructing Congruent Triangles

Using Geometer's Sketchpad

Objective: The students will be able to identify and construct congruent triangles.

Note: This lesson assumes that the concept of similar triangles and the SSS similarity theorem have previously been presented.

Recall the SSS Congruence Theorem: If three sides of one triangle are congruent to three sides of a second triangle, then the triangles are congruent.

This lesson focuses on the construction of congruent triangles using Geometer's Sketchpad.

Upon completion of the following construction, you will be given several exercises to allow you to demonstrate your understanding of congruent triangles and their construction.

Follow the steps listed below to create your own congruent triangles.

1. Open Geometer's Sketchpad to a new sketch.

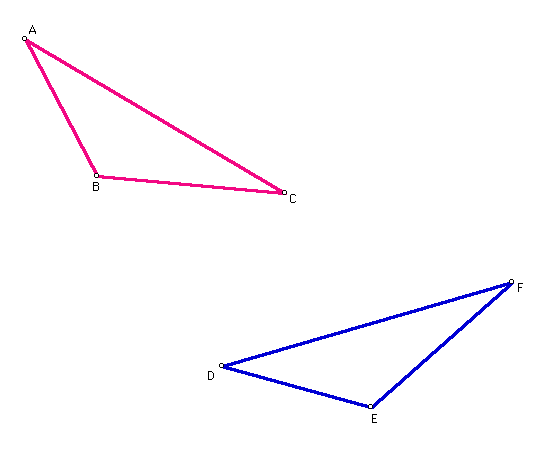
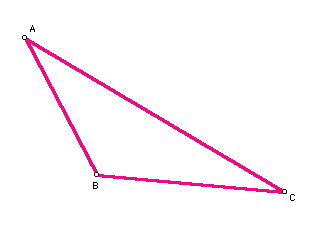
2. Construct a triangle of your choosing. Label its vertices A, B, and C as shown below.
   

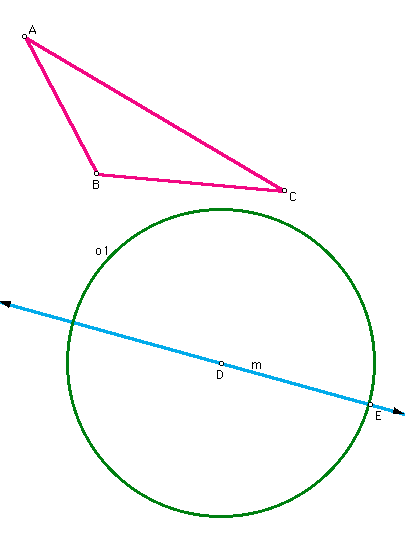
3. Draw a line m NOT touching triangle ABC.

4. Construct a point D on m.

5. Construct a circle o1 with center D and radius AB. (For those unfamiliar with Geometer's Sketchpad, we do this by selecting segment AB and vertex D at the same time (hold down the shift key) and selecting CIRCLE BY CENTER AND RADIUS from the CONSTRUCT menu.) Construct and label vertex E at the intersection of o1 with m. You may see two points of intersection, but we will only be using one of them. (At this point we leave it to the participant to locate and use the construction tools.)
   

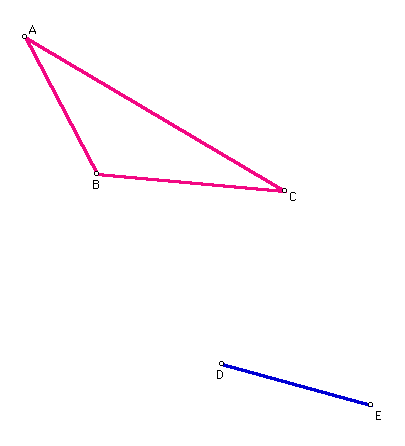
6. Construct segment DE. Hide line m and o1 by selecting m, o1, and HIDE from the DISPLAY menu. You will note that AB and DE are congruent as they have the same length.
   

7. Construct a circle o2 with center D and radius AC.

8. Construct another circle o3 with with center E and radius BC.
   

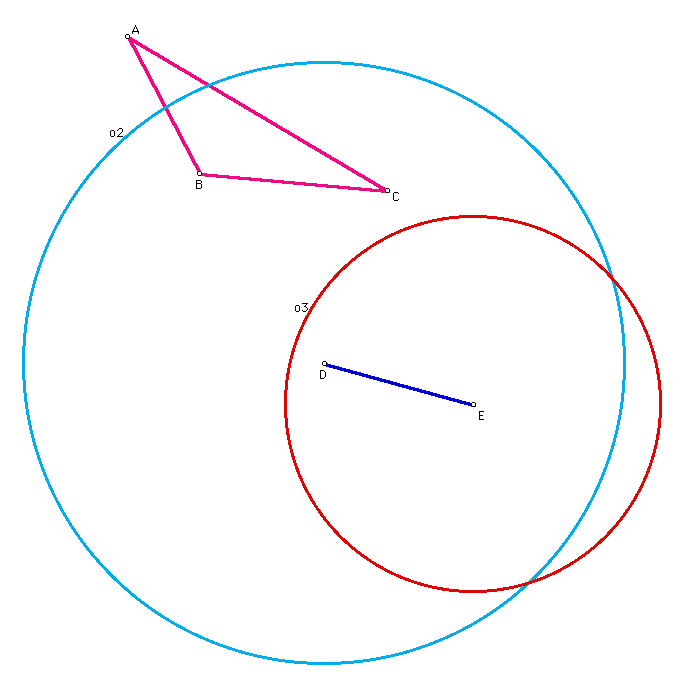
9. Select and label an intersection of o2 and o3 as F. Hide the circles.

10. Construct segments DF and EF. Congratulations! You have just constructed a congruent triangle to ABC.
    

Now that you hae learned how to construct congruent triangles, your mission is to answer the following practice exercise to enhance your skills.

Practice Exercises

1. Which side is congruent to:
   1. AB?
   2. BC?
   3. AC?

2. Which angle is congruent to:
   1. A?
   2. B?
   3. C?

3. Congruent triangles are written in such a way that congruent sides and congruent angles align between triangles. For instance, triangle GHI is congruent to triangle JKL as shown below.
   

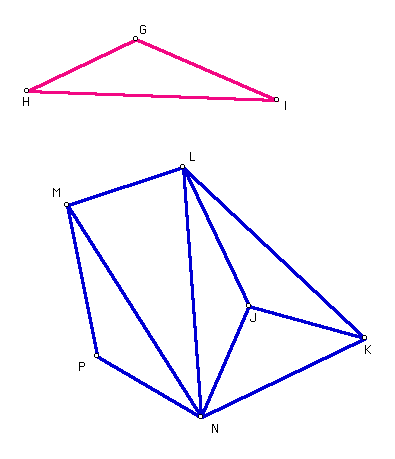
   Fill in the following statements using triangles MNP and LNJ.

   • Triangle GHI is congruent to triangle ______ is congruent to triangle _______.

   • Triangle KJL is congruent to triangle ______ is congruent to triangle _______.

4. Construct triangle QRS as a congruent triangle to triangle MNP shown above. Click on the above image to open it in sketchpad. Save your construction to disk and submit it with your homework.

5. Answer the following statement using triangle GHI.

   Triangle PMN is congruent to triangle ______.

You are now a bonified amateur at congruent triangles and their construction. Continue on in your journey to a deeper understanding of the goemetry around us.