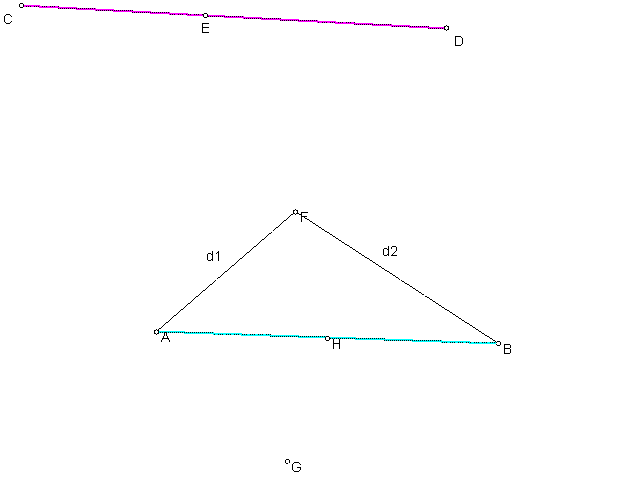
This sketch was based on the fact that a constant distance, K, (represented by CD in the sketch below) can be divided into two parts, d1 and d2=K-d1. The distances d1 and d2 act as the distances from A and B (see the sketch) to a point (x,y) called F on an ellipse, respectively.
The resulting formula is based on the accompanying sketch, where
a=the distance from the center to the point at which the ellipse crosses the x-axis
b=the distance from the center to the point at which the ellipse crosses the y-axis
c=the distance from the center to point A or point B
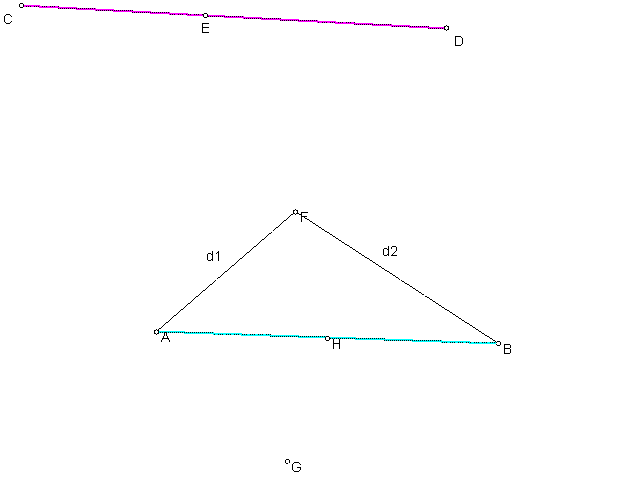
Starting with a, we see that a=SQRT(b^2 + c^2).
Further, d1 + d2 = K = 2a.
But d1=SQRT((x+c)^2 + y^2) and d2=SQRT((x-c)^2 + y^2).
Then SQRT((x+c)^2 + y^2) + SQRT((x-c)^2 + y^2) = 2a.
Switching things around and squaring both sides, we obtain:
Simplifying, we get
Squaring again and simplifying:
Finally, we obtain the equation for an ellipse,
By moving point E, we obtain a collection of points forming an ellipse.

If you would like to see the formation of this ellipse, click here.
Click here to return to Our Group's Homework 2.