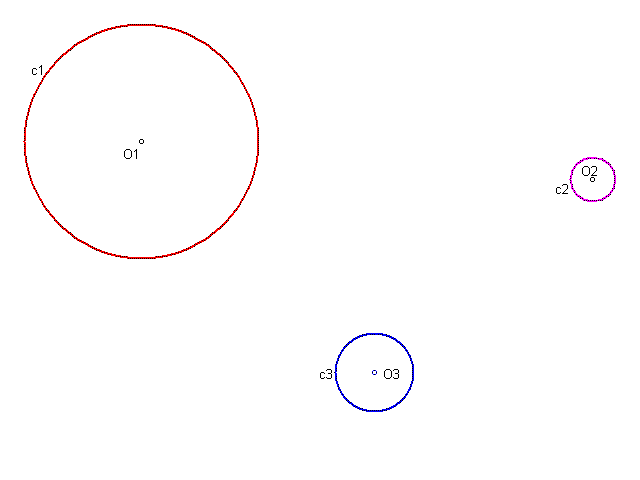

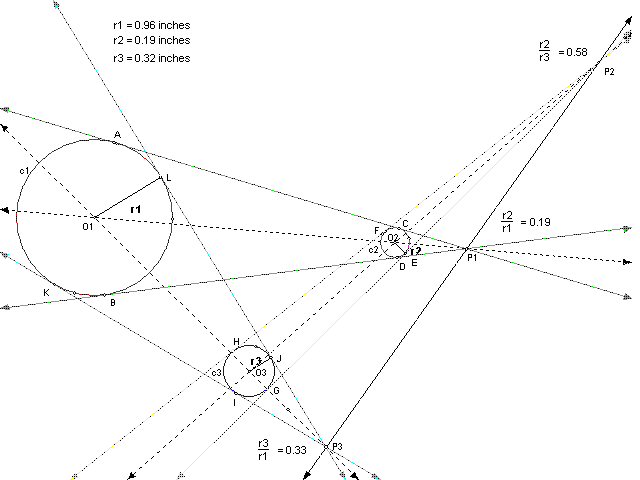
Given three arbitrary disjoint circles of unequal radii, with no one contained in any other, as shown above, a construction similar to the following could be generated:
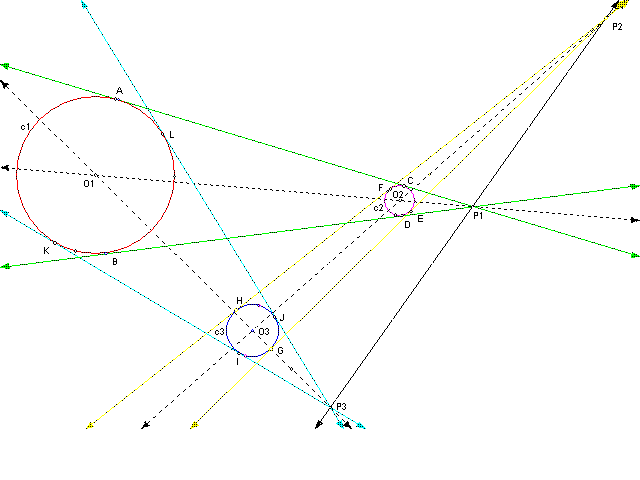
We know that circles are just dilations of each other, and these three are no exception. Further, let us say that these circles are compositions of each other in such a way that the dilation of c1 on center P3 followed by dilation on center P2 is equivalent to the dilation of c1 on center P1.
To show this, we will prove the following:
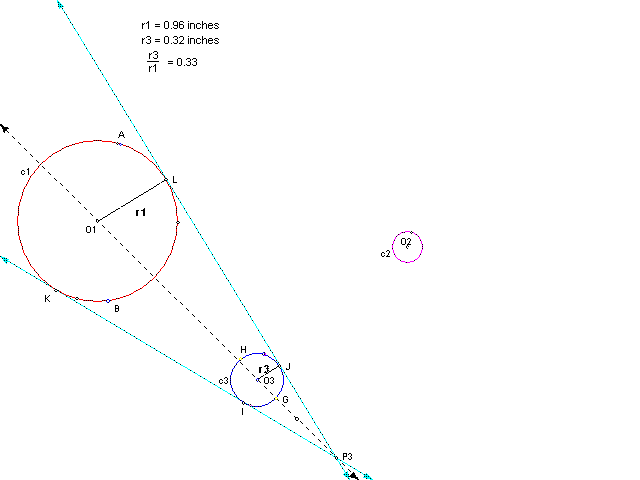
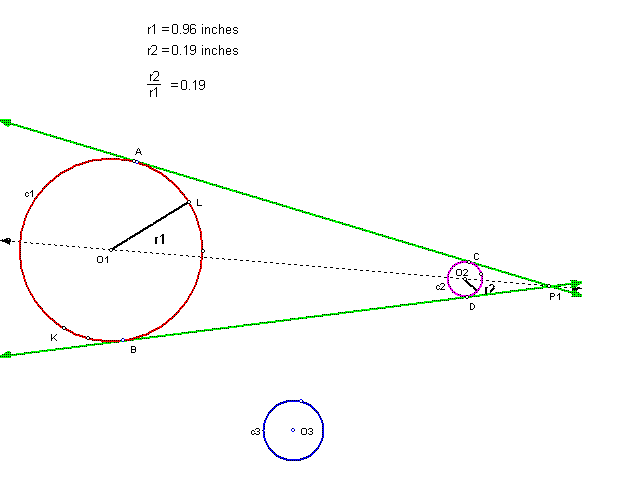
Next we dilate c3 about center P2 giving us c2. The ratio of the radii (thus the scale factor) is 0.58. So, by dilating c1 twice we have composed c2.
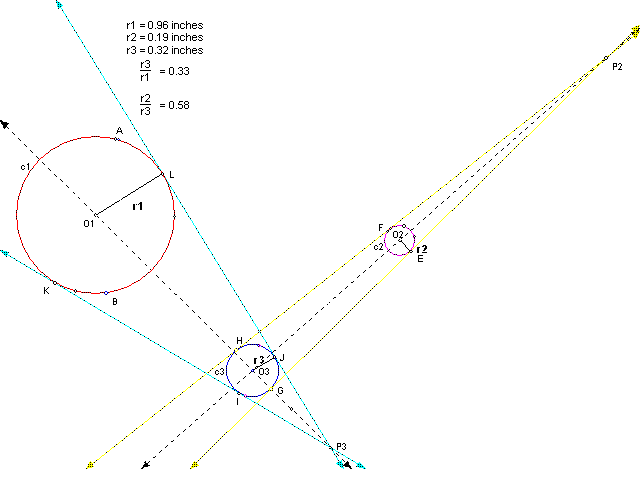
We can also compose c2 by directly dilating c1 about center P1. The ratio of the radii is 0.19.
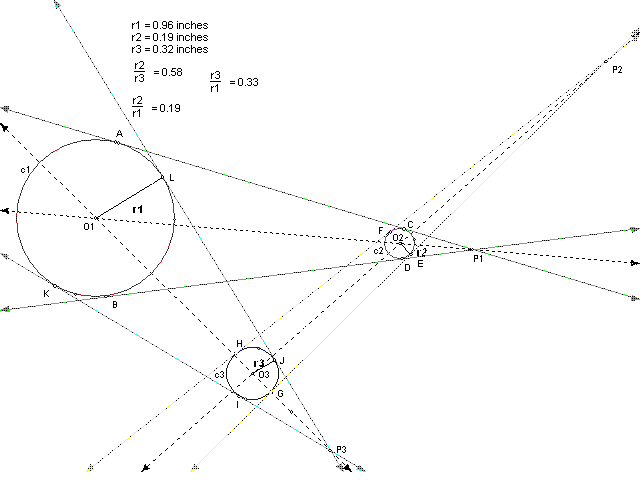
Therefore, by superimposing the previous two sketches, we can show that the composition of two dilations is itself a single dilation. Hence we have proven part 1.
To prove the center of composition (P1) lies on the line between P2 and P3, start with an arbitrary point P, on line m, collinear with P2 and P3.
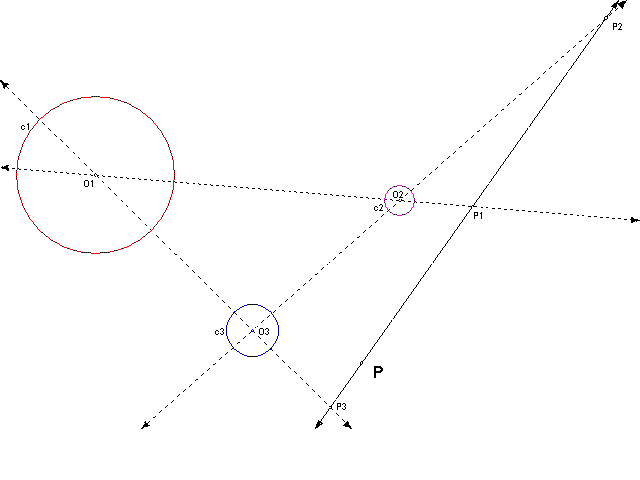
Dilate this point P about any other point on m. As shown below, this dilation d1(P) will also lie on m.
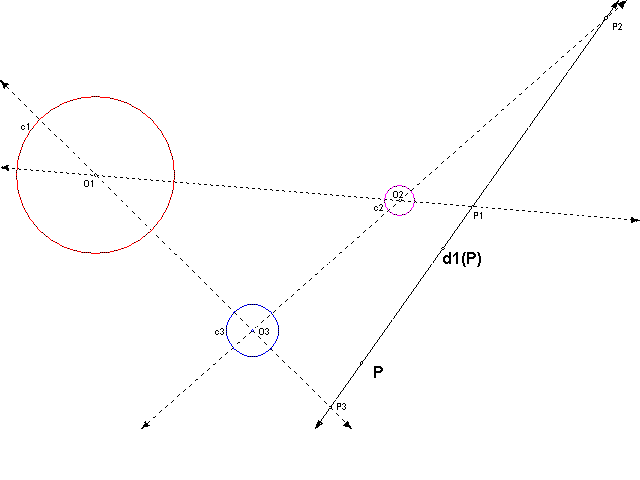
Now dilate d1(P) about any point on m. This dilation d2(d1(P)) will also lie on m.
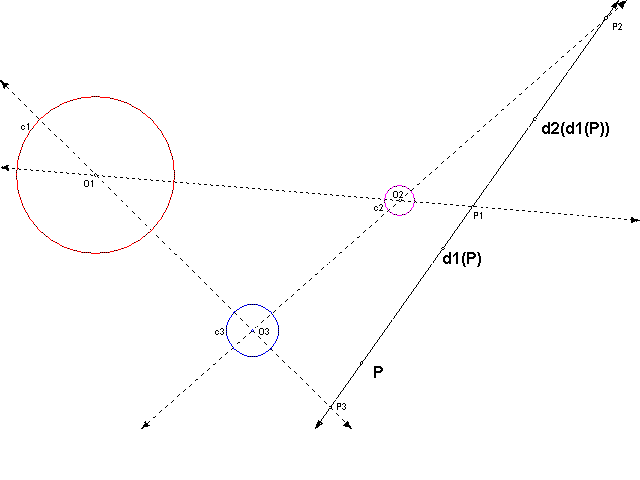
Since all points are collinear, d2(d1(P)) can be constructed directly as d(P).
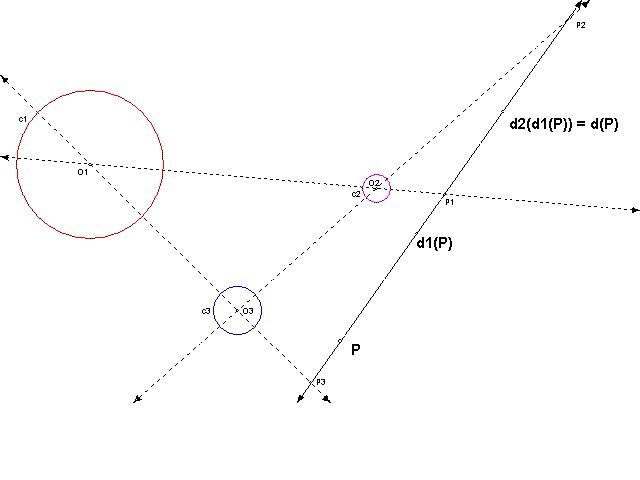
Therefore, Monge's Theorem and the proof are complete!
Click here to return to Our Group's Homework 2.