Solution to Monge's Theorem Problem 4b
In the terminology asked for, the conditions of existence are:
Construct a line containing AA' and another line containing BB'.
- If these lines don't converge, there is no possible dilation.
- If these lines converge in such a manner that A is closer than A' to the convergence point and B is closer than B' to the convergence point, a dilation is possible. Likewise, if these lines converge in such a manner that A' is closer than A to the convergence point and B' is closer than B to the convergence point, a dilation is possible. Otherwise, no dilations are possible.
- If the distance AA' is equal to the distance BB', a dilation is possible. Otherwise, no dilation is possible.
- The center point for dilation will be unique if it does exist.
A better way to approach this and explain why is the following:
To determine existence, answer the following questions:
Construct a line containing AA' and another line containing BB'.
- Do the lines converge?
- YES - see (b)
- NO - STOP. There is definitely not a dilation, since there would be no point to act as center.
- Do they converge in such a manner that A and B are the closest points to the point of convergence?
- YES - see (d)
- NO - see (c)
- Do they converge in such a manner that A' and B' are the points to the point of convergence?
- YES - see (d)
- NO - STOP. No dilation is possible, since the scale factors of A and B are not both either less than or greater than 1.
- Measure distances AA' and BB'. Are they the same?
- YES - STOP. Congratulations! There is indeed such a dilation and it is unique to its mark as center (ie. There is only one point that can be marked as center to obtain A' and B' given A, A', B and B'.)
- NO - STOP. No, there are no dilations here, due to differing scale factors!
The following image illustrates a dilation by a marked ratio.
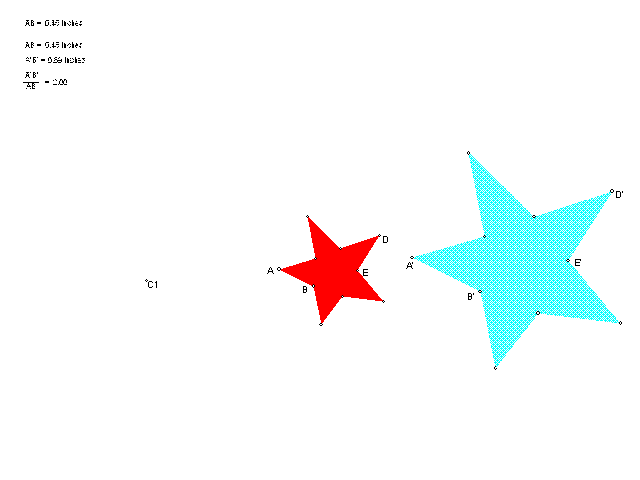
Click on either image to move things around.
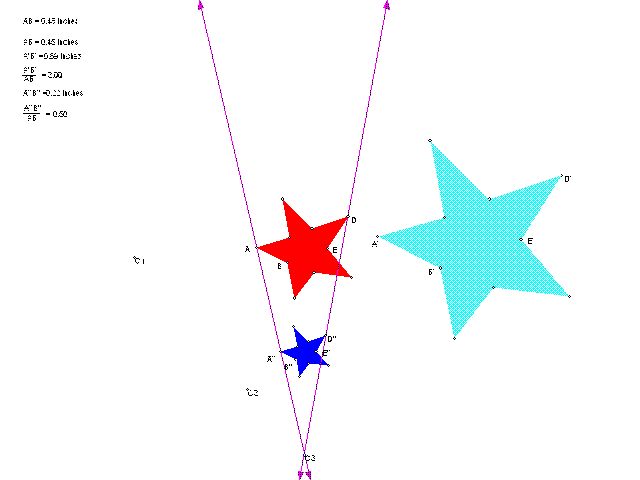
This image shows the composition of two dilations.
Click here to return to Our Group's Homework 2.


