Solution to Monge's Theorem Problem 2

To construct:
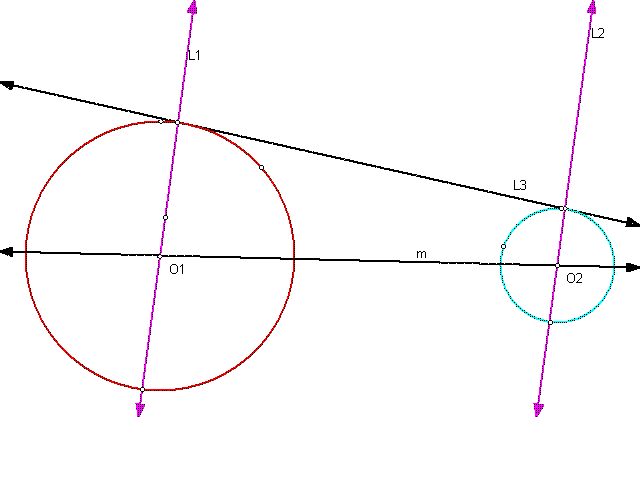
First, construct two circles, c1 and c2, with the first bigger than the second centered at O1 and O2, respectively. Construct line "m" through O1 and O2. Construct line L1 through O1 not passing through O2. Construct a parallel line to L1 passing through O2 but not through O1 called L2. Construct points of intersection between L1 and c1. Do the same for L2 and c2. Construct line L3 through these two newly created points. Label the point of intersection of line L3 with line "m" as Q (see the sketch below). As described in Problem 1's explanation, construct a circle with diameter AO2 and its intersection points, L and N, with the circle c2. To form the tangents to circles c1 and c2, construct a line through LQ and another line through NQ. These lines are shown in the sketch below as t1 and t2 and will cross at point Q. These lines are tangent to circle c1 at points M and P.

Mathematical Facts:

1. (Previously stated) Tangents to a circle are always perpendicular to the radius of the circle.
2. Given that line L1 is perpendicular to line L3. Any line parallel to L1 will also be perpendicular to L3.

Click on the image above to see the trace of L3 as the parallel lines move.

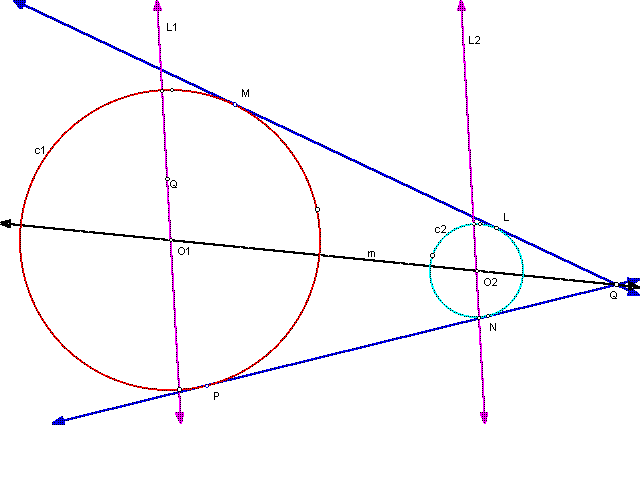
Click on this image to move things around.

Here is the script (for added playing convenience).

Click here to return to Our Group's Homework 2.