Solution to Monge's Theorem Problem 1

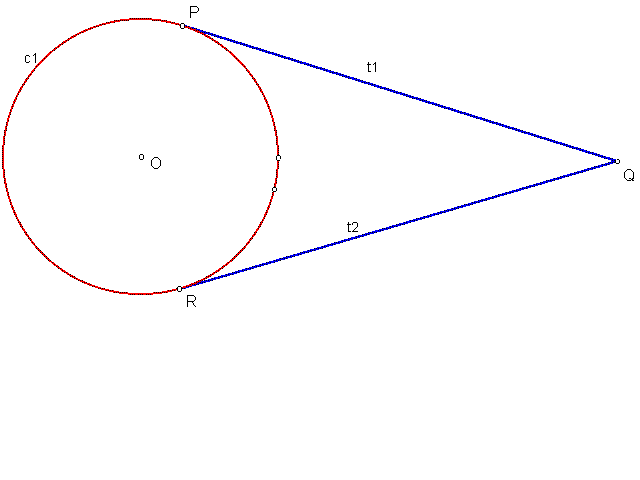
To construct:
First, construct circle c1 with center O and an arbitrary point Q not on the circle. Next, construct a line through O and Q. Construct a segment OQ and it's midpoint N. Then, construct circle c2 using N as its center and ON as its radius. Construct the points of intersection, P and R, between the circles c1 and c2. Finally, construct segments PQ and QR, which are tangent lines to circle c1 through point Q (labeled as t1 and t2 on the following sketch).

Mathematical facts:

1. Tangents to a circle are always perpendicular to the radius of the circle.
2. (More of an explanation of Fact 1 than a fact of its own...) Take a line L1 through O, the center of a circle, and form a perpendicular line L2 through Q, a point not on that line. Let point P be the intersection of L1 and L2. By rotating L1, we see that P traces a circle through O and Q. By Fact 1 (stated above), the line containing QP must be tangent to the circle at the points at which the traces of P cross the circle centered at O in only one location, since L1 contains the radius of the circle and is perpendicular to L2.

Click on the picture to move things around.

Here is the script (for those that like to play).

Click here to return to Our Group's Homework 2.