The Goal:
The Problem:
There are several ways by which to triangulate any given set of points:
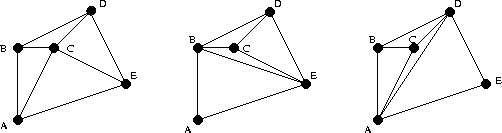
Sometimes we need a triangulation of the points with certain "nice" properties. One of the most common and useful such triangulations is the Delaunay triangulation. Named for the Russian mathematician, Boris Delaunay (originally spelled Delone, and then changed to the French spelling Delaunay), the Delaunay triangulation of a given set of points is defined by the following property:
Equivalently, all triangles in the Delaunay triangulation for a set of points will have empty circumscribed circles. That is, no points lie in the interior of any triangle's circumcircle.
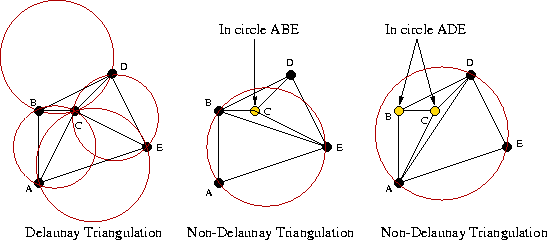
There exists a Delaunay triangulation for any set of points in two dimensions. It is always unique as long as no four points in the point set are co-circular. Because it minimizes small angles and circumscribed circles, the Delaunay triangulation is geometrically nice and, in general, pleasing to the eye.
It is important to note that we ultimately wish to generate constrained Delaunay triangulations. That is, we want to be able to compute a modified version of the Delaunay triangulation in which user-defined edges or "constraints" may be specified. Since the Delaunay triangulation is unique for any point set (with the exception of sets with co-circular points), the constrained Delaunay triangulation will most likely contain some edges which are not Delaunay.
Further Information About Delaunay Triangulations:
- http://www.ifor.math.ethz.ch/ifor/staff/fukuda/polyfaq/node13.html
- http://tamfana.informatik.uni-dortmund.de/RVS/MA/Stud/misch/applets/Delaunay/Delaunay.html
- http://www.gris.uni-tuebingen.de/gris/proj/dt/dteng.html
The Algorithms:
- Generating the Delaunay Triangulation
To generate the Delaunay triangulation, we chose to implement a "divide and conquer" algorithm presented by Guibas and Stolfi , in:
Guibas, L. and Stolfi, J., "Primitives for the Manipulation of General Subdivisions and the Computation of Voronoi Diagrams", ACM Transactions on Graphics, Vol.4, No.2, April 1985, pages 74-123.
The divide and conquer algorithm only computes the Delaunay triangulation for the convex hull of the point set. The first step is to put all of the points into order of increasing x-coordinates (when two points have the same x-coordinate, their order is determined by their y-coordinates).
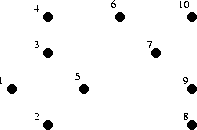
This set of 10 points has been ordered
Once the points are ordered, the ordered set is successively divided into halves until we are left with subsets containing no more than three points. These subsets may be instantly triangulated as a segment in the case of two points and a triangle in the case of three points.
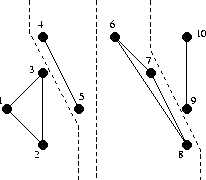
The set has been "halved" into subsets of 2 or 3 points and the subsets have been triangulated individually
From here, the triangulated subsets are recursively "merged" with their former other halves. The final product of any merge will be a triangulation consisting of LL-edges (edges previously present in the left triangulation, having endpoints from the left subset), RR-edges (edges previously present in the right triangulation, having endpoints from the right subset), and LR-edges (new edges running between the left and right triangulations, having one endpoint from the left subset and one endpoint from the right subset). To maintain Delaunayhood over the merged point subsets, deletion of LL and RR-edges may be necessary. However, we never create new LL or RR-edges, when merging.
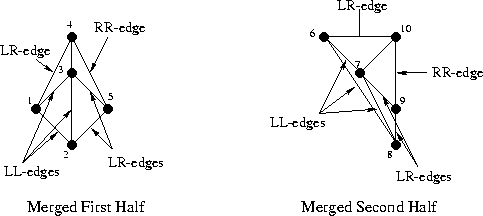
The first two merges are shown here. They were somewhat simple, with no deletion of any LL or RR-edges in either case. The next merge will prove to be a bit more complicated and demonstrative of the algorithm
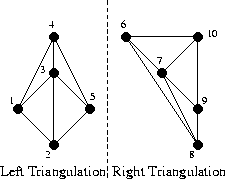
Here is our triangulation so far, with one more merge remaining. All edges in the left triangulation are LL-edges and all edges in the right triangulation are RR-edges.
The first step for merging the two halves is to insert the base LR-edge. The base LR-edge is the bottom-most LR-edge which does not intersect any LL or RR-edges.
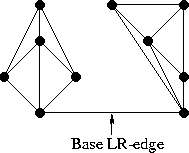
The base LR-edge between the right and left triangulations
Working upward from here, we need to determine the next LR-edge to be added just above the base LR-edge. Clearly, such an edge will have, as one endpoint, either the left or right endpoint of the base LR-edge. The other endpoint, then, will come either from the left or the right point subset. Naturally, we narrow our decision by selecting two candidate points: one from the left subset and one from the right subset.
Let us begin with the right side. The first potential candidate is the point connected to the right point of the base LR-edge by the RR-edge which defines the smallest clockwise angle from the base LR-edge. Similarly, the next potential candidate defines the next smallest clockwise angle from the base LR-edge.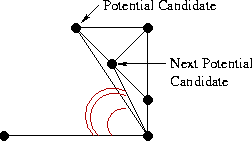
Selection of the initial potential and next potential candidates
The potential candidate is then checked for the following two criteria:- The clockwise angle from the base LR-edge to the potential candidate must be less than 180 degrees.
- The circumcircle defined by the two endpoints of the base LR-edge and the potential candidate must not contain the next potential candidate in its interior.
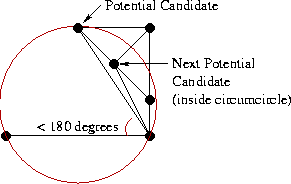
Here, the potential candidate satisfies the first criterion, but not the second.
If both criteria are satisfied, the potential candidate becomes our final candidate for the right side. If the first criterion does not hold, then no candidate for the right side is chosen. If the first criterion holds but the second does not, then the RR-edge from the potential candidate to the right endpoint of the base LR-edge is deleted. The process is then repeated with the next potential candidate as the potential candidate until a final right candidate is chosen or it is determined that no candidate will be chosen.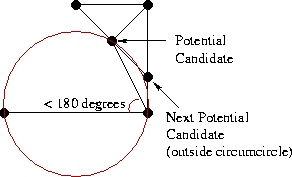
After deleting the "bad edge," a suitable right candidate is found.
As for the left candidate selection, the process is just the mirror image of that for the right.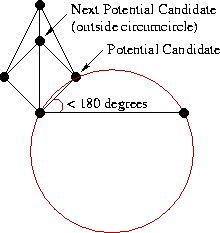
On the left side, the initial potential candidate satisfies both criteria.
When neither a right nor a left candidate is submitted, the merge is complete. If only one candidate is submitted, it automatically defines the LR-edge to be added. In the case where both candidates are submitted, the approprate LR-edge is decided by a simple test: if the right candidate is not contained in interior of the circle defined by the two endpoints of the base LR-edge and the left candidate, then the left candidate defines the LR-edge and vice-versa. By the guaranteed existence of the Delaunay triangulation (here applied to only four points), at least one of the candidates will satisfy this; by the uniqueness of the Delaunay triangulation, only one candidate will satisfy this (except in the case when the four points are co-circular).
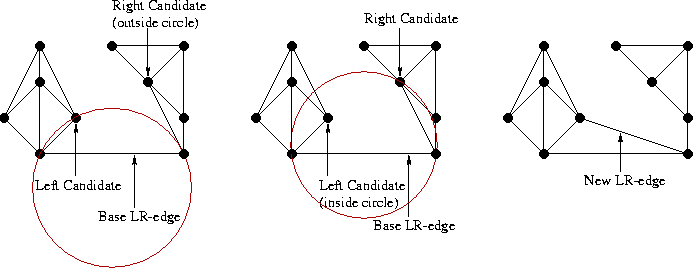
In this example, only the left candidate satisfies the condition, and thus defines the new LR-edge.
Once the new LR-edge is added, the entire process is repeated with the new LR-edge as the base LR-edge.
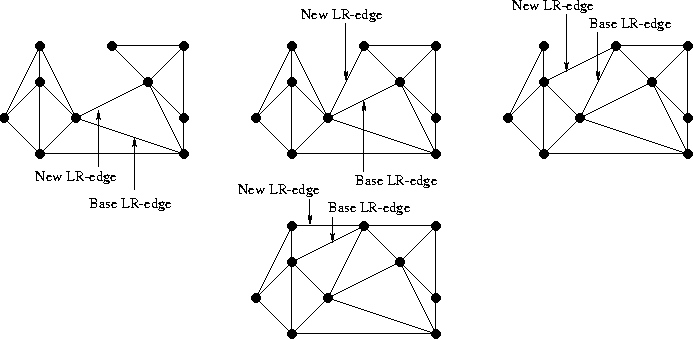
LR-edges are added until the merge is complete (i.e. until no left or right candidates are submitted)
Finally, once the last two halves (those that resulted from the first "halving" of the point set) are merged, the Delaunay triangulation is complete.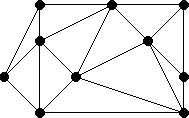
The Delaunay Triangulation
Examples of Delaunay triangulations:
Next, the constraints are added to the Delaunay triangulation. Constraints will all be in the form of a required edge between two points. To adjust for the constraint, we need to delete all triangles which have an edge that intersects the constraint. In a way, we are clearing a path for the constraint. Once this is finished, we will have a polygon, within our triangulation, that contains the two points of the constraint.
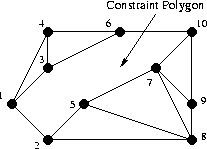
A path is cleared for the constrained edge 1->10, giving a polygon.
The constrained edge is then added.
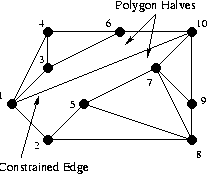
The addition of the constrained edge cuts the polygon into two pieces.
The two pieces are then triangulated generically, giving us back a triangulation.
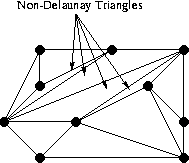
The new triangulation is no longer entirely Delaunay.
This process is then repeated for all constrained edges.
Holes in the triangulation may be specified as a closed polygon consisting of constrained edges. Once the constraints are in place, we may invoke a "triangle-eating virus" which erases all triangles inside the polygon.
Examples of constrained Delaunay triangulations:
The Implementation:
Taking an object oriented approach to this problem, we chose to implement the algorithm in C++. There is a slight duality, in that our data structures for implementing the divide and conquer Delaunay generator are different than those for implementing the addition of constraints.
For calculating the Delaunay triangulation, we used a modified version of the triangular data structure given by Jonathan Richard Shewchuk, in:
Jonathan Richard Shewchuk, "Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator," First Workshop on Applied Computational Geometry (Philadelphia, Pennsylvania), pages 124-133, Association for Computing Machinery, May 1996.
The triangle is defined by six data members: three vertices and three neighboring triangles. In the case that the triangle is degenerate, that is it has only two vertices, we assign the third vertex to be null. Each triangle is created so that vertex one is the lowest of the three in the point ordering, and vertex two is clockwise from vertex one and vertex three is clockwise from vertex two. The pointers to neighboring triangles are ordered so that Adjacent Triangle 1 is opposite vertex one, and so on.
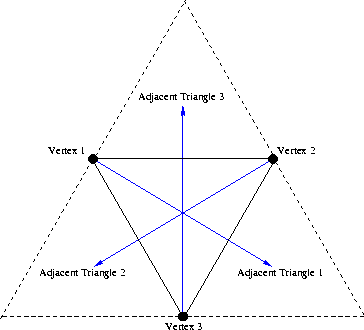
If there is no adjacent triangle opposite a vertex, then the neighboring triangle is assigned to be the first triangle encountered on a path from the said vertex, outside the triangle and revolving counter-clockwise about the vertex which is clockwise from the said vertex.
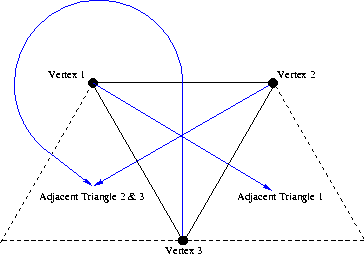
This data structure allows for a triangulation to remain connected (that is all triangles can be accessed starting with any given triangle), even when it is incomplete.
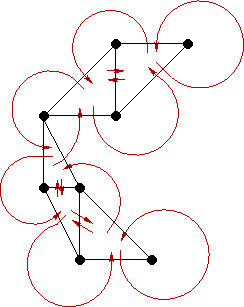
The data structure just described works very well for implementing Guibas' and Stolfi's algorithm for finding the Delaunay triangulation. When it comes to adding the constraints, however, complications arise. We will show by example just how the data structure breaks down when it comes to adding the constraints and demonstrate the benefits of the alternative.
Suppose we have the following Delaunay triangulation, generated by the algorithm from Guibas and Stolfi, using the above described triangular data structure: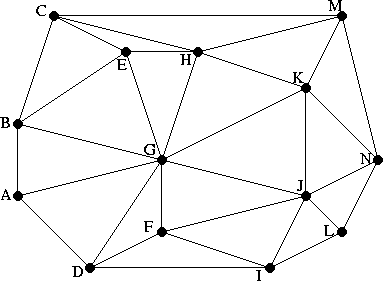
Suppose, now, that we would like to add the constrained edge BL.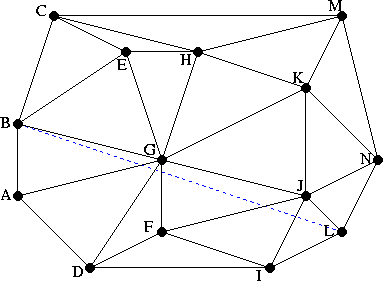
Following the algorithm described earlier, the first step is to delete all triangles which intersect the constrained edge.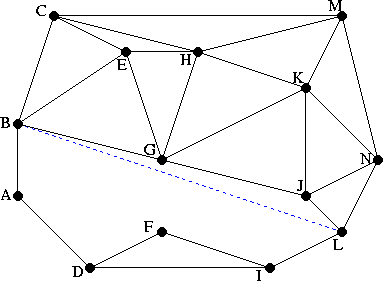
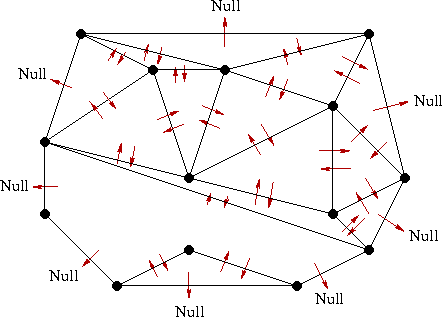
According to the triangular data structure, our triangulation will maintain its connectedness by way of "ghost" triangles (triangles with a null endpoint) and circular arrows.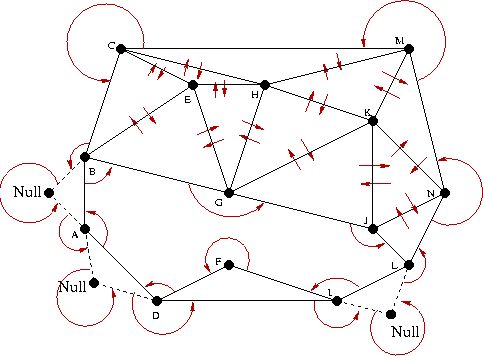
Also, since we will need to re-triangulate and then replace the deleted region, it too needs to be stored, triangulated to include the constrained edge, and represented.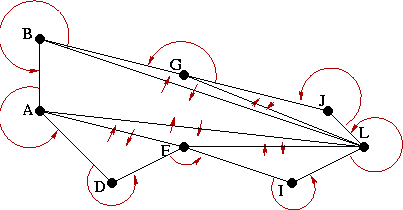
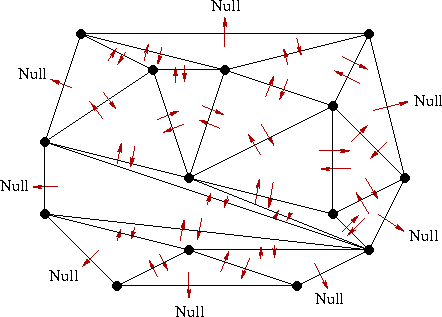
Now that the region has been re-triangulated, it must be added back into the big picture like a piece in a puzzle. This is where the difficulty erupts. Pictorally, it is easy to see how things fit together. When it comes to the internal representation, however, matching up adjacent triangles and resetting pointers is a very exhaustive process especially when "ghost" triangles and non-adjacent triangles are involved. It is a hassle which grows with the number of points and constraints. Clearly, our data structure needs modification when it comes to adding constraints.
The solution lies within a more general, flexible data structure: the polygon. The polygon is similar to the triangle data structure in that its data members consist of vertices (ordered clockwise) and adjacent polygons, with the addition of a variable size (meaning the number of vertices). One big difference between these two structures, besides the variable size of the polygon, is that the polygon only contains references to polygons immediately adjacent to it. In the case that one side has no adjacent polygon, the pointer is set to null. Also, since our polygon is not necessarily convex, we cannot assign the sides by the vertices opposite them. Instead, edge one is assigned to be the edge between vertex one and vertex two, and so on, and finally, edge n (where n is the size of the polygon) is assigned to be the edge between vertex n and vertex one.
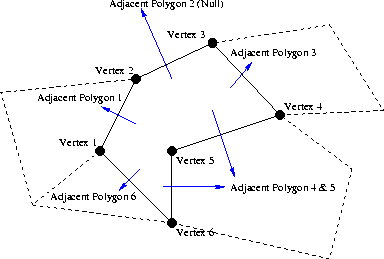
This data structure is nice in that it is commutative. That is, if polygon A has a reference to polygon B, then it follows that polygon B must have a reference to polygon A.
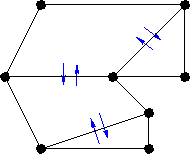
The key to the structure's success in solving our problem, lies within two of the mutator functions for the polygon: split and join.
The split function splits a polygon into two adjacent polygons along a specified edge.
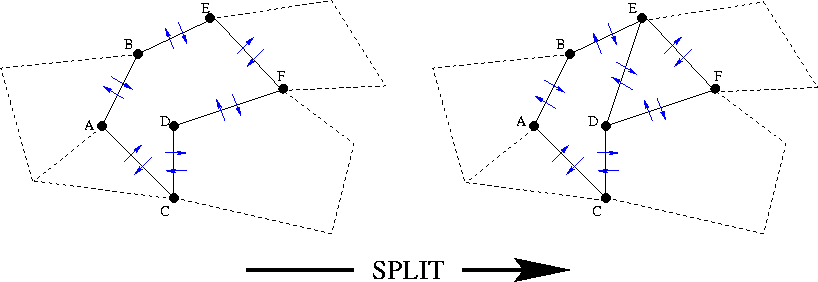
The join function fuses two adjacent polygons into one polygon.
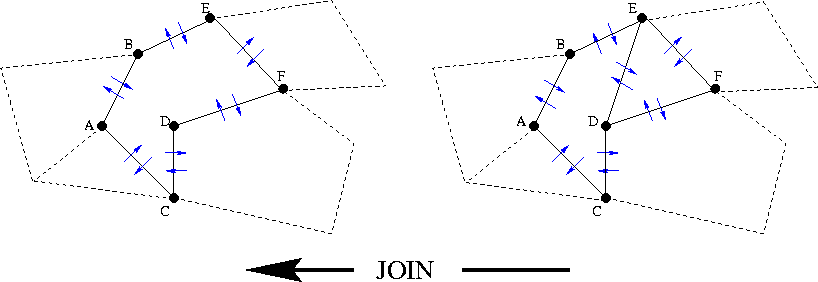
Clearly, these two functions are just opposites of one another. These simple mutators can be readily applied to our edge constraint problem (of course, once all triangles in the triangulation have been converted into polygons).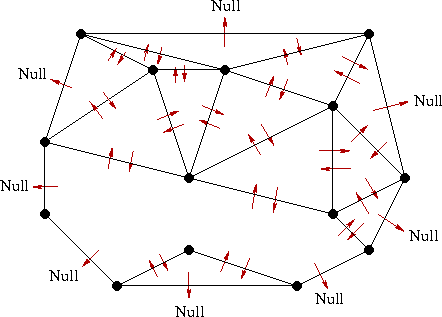
Applications:
- High Quality Triangular Meshes:
Very often in computer graphic design, differential equations problems, and numerical analysis, it is necessary to triangulate points in a given problem region into a high-quality mesh. By high-quality, we mean a triangulation with relatively uniform triangles. That is, we would like to exclude triangles with extremely small (and large) angles. An algorithm for solving this problem in two and three dimensions is presented by L. Paul Chew, in his paper, "Guaranteed High-quality Mesh Generation for Curved Surfaces." The first step in the algorithm is to generate the constrained Delaunay triangulation for the given set of points. Once this is done, the remainder of the algorithm consists of a simple but elegant "grading" of the triangles and successively adding points into the triangulation.
- Minimum Spanning Trees:
In many combinatorial problems, it is helpful to know the minimum spanning tree for a given set of points in the plane; that is, a spanning tree with minimum total edge length. It has been proven that every minimum spanning tree of a set of points, S, is a subgraph of the Delaunay triangulation of S.
- Voronoi Diagrams:
Named for the Russian mathematician, Georges Voronoi, Voronoi diagrams are also known as Thiessen Polygons and Blum's Medial Axis Transform. The Voronoi diagram for a set of points, S, in two dimensions (assuming no three colinear or four cocircular points) is a division of the plane into polygons. Each point in S is in the interior of some polygon and every polygon contains exactly one point in its interior. Each polygon steaks out the region which is closer to its contained point than to any other point in S.
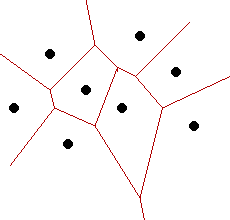
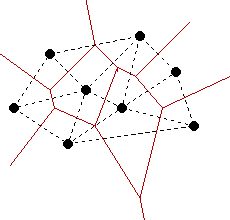
The Voronoi diagram is actually the straight-line dual of the Delaunay triangulation. That is, we can go from the Voronoi diagram to the Delaunay triangulation by drawing in the edges which are perpendicular to the region boundaries and vice-versa.
Acknowledgments:
- This project was completed as part of the Minnesota Center for Industrial Mathematics Undergraduate Industrial Mathematics Project.
- The problem was put forth by XOX corporation of Minnesota.
- Advisors for this project were:
- Jesus De Loera, Postdoctoral Fellow at the University of Minnesota
- Wojciech Komornicki , Professor of Mathematics at Hamline University
- Jesus De Loera, Postdoctoral Fellow at the University of Minnesota
- Special thanks to The Geometry Center of the University of Minnesota for use of their computing facility.
Go to my home page
To request source code or for any other reason, click here:samuelp@geom.umn.edu