COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS

IN THE PLANE

By Samuel Peterson, University of Minnesota Undergraduate

Applications
The Goal
The Problem
The Algorithms
The Implementation
Acknowledgments

Slide 2

Applications:

Voronoi Diagrams
Minimum Spanning Trees
High Quality Triangular Meshes

Slide 3

The Goal:

Implement an algorithm for finding the constrained Delaunay triangulation of a given point set in two dimensions.

The Problem:

There are several ways by which to triangulate any given set of points:

There are three possible triangulations of this set of points.

Slide 4

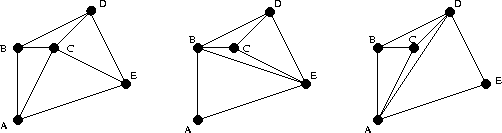
Slide 4

The Delaunay triangulation of a given set of points is defined by the following property:

AB is an edge of the Delaunay triangulation iff there is a circle passing through A and B so that all other points, C, where C is not equal to A or B, lie outside the circle.

Equivalently, all triangles in the Delaunay triangulation for a set of points will have empty circumscribed circles.

Slide 5

The Algorithms:

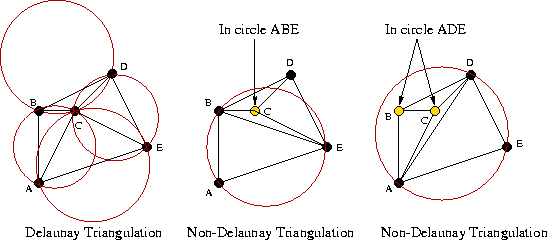
Generating the Delaunay Triangulation

To generate the Delaunay triangulation, we chose to implement a "divide and conquer" algorithm presented by Guibas and Stolfi , in:

Guibas, L. and Stolfi, J., "Primitives for the Manipulation of General Subdivisions and the Computation of Voronoi Diagrams", ACM Transactions on Graphics, Vol.4, No.2, April 1985, pages 74-123.
Adding Constraints

Slide 6

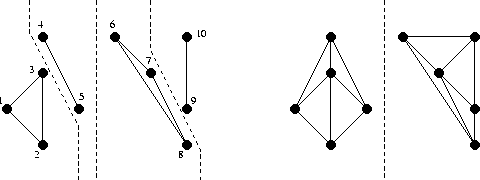
Slide 7

Examples of Delaunay Triangulations

Slide 8

Slide 8
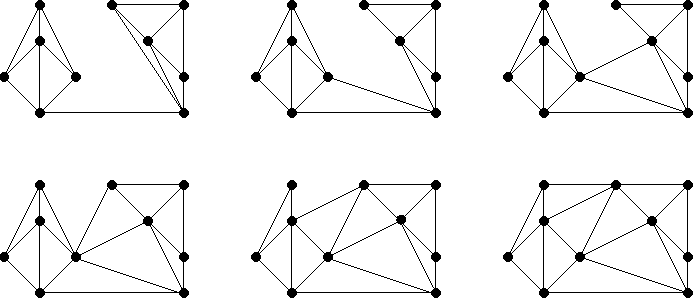
Next, the constraints are added to the Delaunay triangulation. To adjust for the constraint, we need to delete all triangles which have an edge that intersects the constraint.

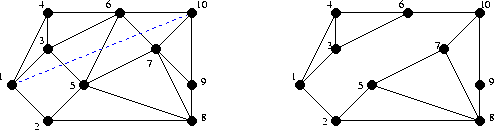
The constrained edge is then added, and the region is re-triangulated (this time generically).

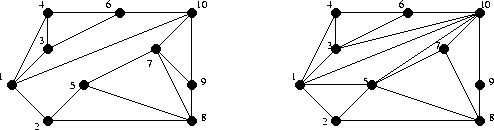
Slide 9

Examples of Constrained Delaunay Triangulations

Slide 10

The Implementation:

Finding the Delaunay Triangulation
For calculating the Delaunay triangulation, we used a modified version of the triangular data structure given by Jonathan Richard Shewchuk, in his paper, "Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator."

Slide 11
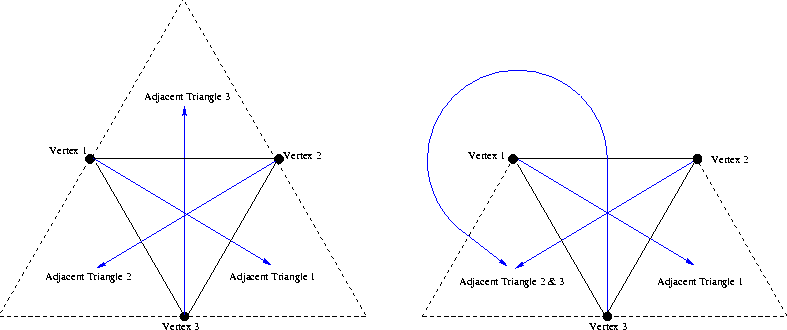
Slide 11

This data structure allows for a triangulation to remain connected (that is all triangles can be accessed starting with any given triangle), even when it is incomplete.

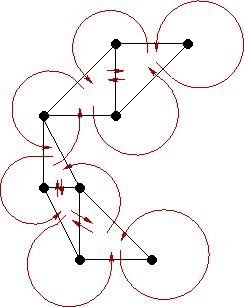
Slide 12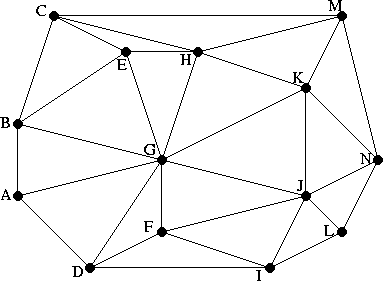
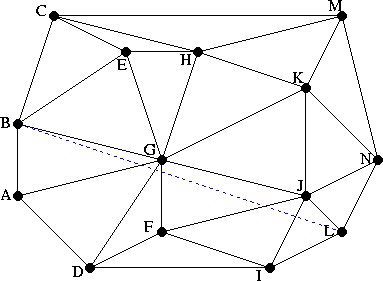
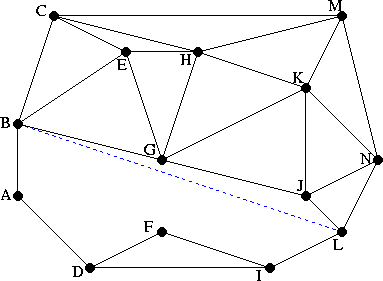
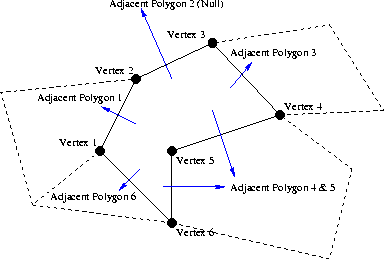
Adding the Constraints

According to the triangular data structure: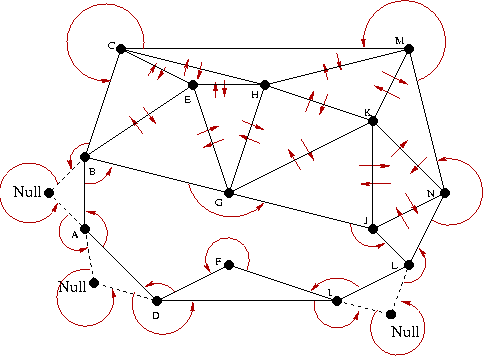 Slide 13
A New Data Structure: The Polygon

Slide 14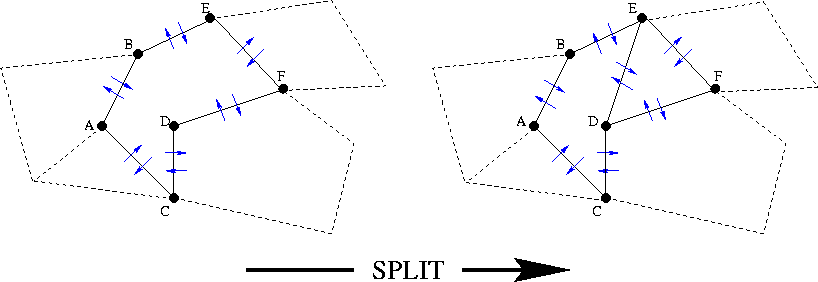
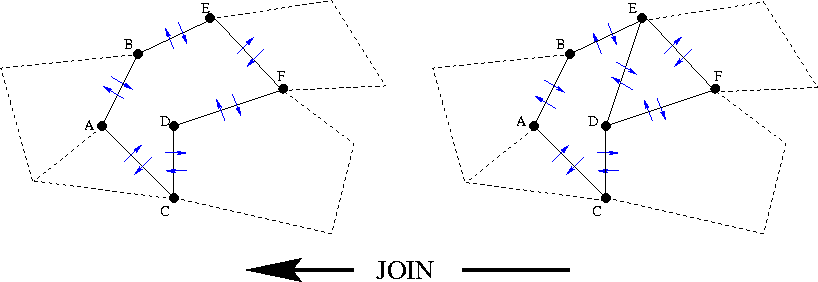
Slide 14

Slide 15
Slide 15

Slide 16

Acknowledgments:

This project was completed as part of the Minnesota Center for Industrial Mathematics Undergraduate Industrial Mathematics Project.
The problem was put forth by XOX corporation of Minnesota.
Advisors for this project were:
- Jesus De Loera, Postdoctoral Fellow at the University of Minnesota
- Wojciech Komornicki , Professor of Mathematics at Hamline University
Special thanks to The Geometry Center of the University of Minnesota for use of their computing facility.