Finding Orbits: Introduction to the Mathematical Ideas

Building a System Model

To approach the problem of locating the libration points and the orbits around them, the first step is of course to build a mathematical model of the earth-sun-spacecraft system. Specifically, one wants to find equations which describe the motion of the spacecraft due to the graviatational field induced by both the earth and the sun. Here are the main steps in composing this model:
  1. Use Newton's Universal Law of Gravitation to write the equations for the force on the spacecraft induced by the earth and the force on the spacecraft induced by the sun.
  2. Becuase superposition of forces holds in the physical universe, the total force on the spacecraft in the earth-sun system is the sum of the forces induced individually by the earth and sun
  3. The force on the spacecraft is its mass times its acceleration, which yields a vector equation (or alternatively, 3 equations: x(t), y(t), and z(t) ) for it's motion in terms of the masses and motions of the earth and the sun.
  4. Several coordinate transformations are applied to the equations to make them easier to work with and to remove time from explicitly appearing in the transformed equations. These transformations are:

When these steps are completed, the equations of motion for the spacecraft are as follows:

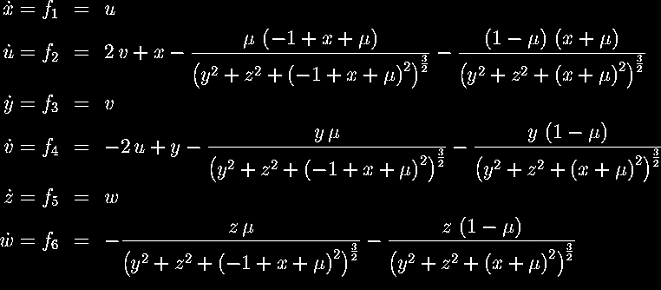
The next step is to use these equations to find the libration points of the system.


Computing the Libration Points