Multivariable Calculus (Math 3354)
Rick Wicklin
Rick's Office: 451 Vincent Hall, 626-8308 or 626-1324
fjw@geom.umn.edu, http://www.geom.umn.edu/~math335x
Textbook: Multivariable Calculus by Damiano and
Freije, Brooks-Cole, 1996.
Text for sale ($20) at the Special Projects Office, 115 VinH, 8:30-4:00pm.
TAs: Bob Hesse (Workshop Czar)
Sec 1 (9:00-9:55): E. Schirmacher
Sec 2 (11:15-12:05): G. Naughton
Sec 3 (13:25-14:15): T. Brule
This course will focus on the geometry of curves and surfaces (and
related differential equations) for the first six weeks of the course.
The remainder of the course will focus on the local linear
approximation of a function or a vector field.
- Week 1
- (9/26-10/3)The Geometry of Parametric Curves
- Read §3.1,3.3 and §2.1-2.3.
- Vectors, parametric lines, tangent vectors to curves,
velocity vectors, chain rule for g(f(t)) where
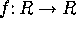 ,
,
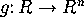 . The difference between a graph and an image, and
between slope and a tangent vector.
. The difference between a graph and an image, and
between slope and a tangent vector. - Linear Algebra: Review of basic vector concepts.
- Graded Lab: (Lab 1) Introduction to Maple derivatives, vector notation, plotting
planar graphs and images, plotting spacecurves, printing.
- Homework: (HW 1) Families of parametric curves.
- Workshop topics:
- Inventing a parametrization of simple planar and nonplanar curves.
Can different parametrizations have the same image?
Computing of the velocity vector based at the point of tangency.
- Parametrized curves arising from solution of simple (uncoupled)
linear ODEs.
- Weeks 2-3
- (10/4-18) The Geometry of Surfaces in
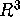
- Read §1.1-1.2 and §4.2-4.3.
- Graphs of
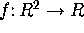 , planes as graphs, coordinate curves,
slope in coordinate directions (=partial derivatives),
directional derivatives and the gradient.
Parametrized surfaces and
tangent vectors to coordinate curves on surface.
, planes as graphs, coordinate curves,
slope in coordinate directions (=partial derivatives),
directional derivatives and the gradient.
Parametrized surfaces and
tangent vectors to coordinate curves on surface. - Linear Algebra: (NEW!) linear combination (span) of vectors
- Graded Lab: (Lab 3)
Exploring the geometry of surface graphs and directional
derivatives by examining ``cross-section'' of surfaces.
- Homework: (HW 2) Construct a surface; (HW 3) Numerical estimates of
directional derivatives.
- Workshop topics:
- Discussion 4.1
- (Lab 2) Parametrizing planes in Maple
- Discussion 4.3
- GATEWAY I
- 10/17
- EXAM I
- 10/22. Covers weeks 1-3.
- Week 4
- (10/23-29) Max/Min/Saddles
- Read §4.5, 5.1, 5.2
- Critical points and how to find them, types of critical points
(saddle versus extremum), gradient vector fields and
their equilibria, optimization of scalar functions.
- Linear Algebra: review of orthogonality of two vectors.
- Graded Lab: (Lab 5)
Relationship of a gradient vector field,
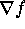 , to the
graph of f. Discovering linear phase portraits of
nodes and saddles.
, to the
graph of f. Discovering linear phase portraits of
nodes and saddles. - Homework: (HW 4) Gradients; (HW 5) Discussion 5.2
- Workshop topics:
- Discussion 4.4
- (Lab 4) Intro to Matlab and PPLANE
- Discussion 5.1
- Locating and classifying critical points. Second derivative test.
- Are all vector fields gradient fields? How can we tell
geometrically and analytically whether a vector field is gradient?
- Weeks 5-6
- (10/30-11/13) Level Sets
- Read §4.5, 5.3
- Implicit curves, gradient vector fields revisited,
Hamiltonian vector fields, implicit differentiation,
change of topology across singular levels,
Lagrange multipliers.
- Graded Lab: (Lab 7) Planetary motion (Kepler's restricted planar 2- and 3-body
problem)
- Homework: (HW 6) Changing topology as levels change and relating that change to
critical points on the graph of the function; (HW 7) Lagrange
multipliers (letter to boss)
- Workshop topics:
- Relationship of gradient and Hamiltonian vector fields
to the geometry of surfaces.
- (Lab 6) The geometry of the gravitational potential function.
- Discussion 5.3: The geometry of Lagrange multipliers.
- GATEWAY II
- 11/12
- EXAM II
- 11/14 Covers weeks 1-6, with an emphasis on weeks 4-6.
- Weeks 7-8.5
- (11/15-11/21) Tangent Planes
- Read §4.1, 4.4
- Multivariable limit, limit along a curve, notions of continuity
and differentiability, existence of tangent plane, tangent plane
at critical points.
- Linear Algebra: review linear independence, span, linear combinations.
matrix-vector multiplication.
- Brainfood:
- Differentiable and non-differentiable surfaces.
- Different ways to compute tangent planes to surfaces:
Relationship between tangent planes to graphs,
and to parametrized surfaces. Verification of
tangent plane to implicitly-defined surfaces.
- Weeks 8.5-10
- (11/22-12/6) Linear Approximations and Jacobians
- Read ??
- Tangent plane as best affine approximation to surface,
Recognition of
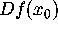 as a linear map,
Jacobian as best affine approx for vector field at equilibria,
general chain rule: D(f(g(x))= Dg(f(x)).Df(x) (requires param. surfaces)
as a linear map,
Jacobian as best affine approx for vector field at equilibria,
general chain rule: D(f(g(x))= Dg(f(x)).Df(x) (requires param. surfaces) - Graded Lab:
Comparison of trajectories of Hamiltonian vector fields
and the vector field obtained by linearization at equilibrium.
Relate to geometry of generating function.
- Brainfood:
- Comparison of level sets for
nonlinear function and the linear approximation at a critical point.
- Composing a parametrized curve with a parametrization of a surface
and using the chain rule to compute derivative information.
- GATEWAY III
- 12/3
- FINAL EXAM
- 12/9, 1:30pm, AndH 350. The final exam covers material
from weeks 1-10 with a slight emphasis on weeks 7-10.
About this document
Return to Calculus 3353/3354 Homepage
URL: http://www.geom.umn.edu/~math335x/Syllabus1/Syllabus1.html
Copyright: 1996 by the Regents of the University of Minnesota.
Department of Mathematics. All rights reserved.
Comments to:
hesse@math.umn.edu
Last modified: Wed Nov 27 17:23:07 1996
The University of Minnesota is an equal opportunity educator and employer.
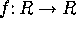 ,
,
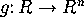 . The difference between a graph and an image, and
between slope and a tangent vector.
. The difference between a graph and an image, and
between slope and a tangent vector.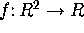 , planes as graphs, coordinate curves,
slope in coordinate directions (=partial derivatives),
directional derivatives and the gradient.
Parametrized surfaces and
tangent vectors to coordinate curves on surface.
, planes as graphs, coordinate curves,
slope in coordinate directions (=partial derivatives),
directional derivatives and the gradient.
Parametrized surfaces and
tangent vectors to coordinate curves on surface.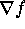 , to the
graph of f. Discovering linear phase portraits of
nodes and saddles.
, to the
graph of f. Discovering linear phase portraits of
nodes and saddles.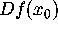 as a linear map,
Jacobian as best affine approx for vector field at equilibria,
general chain rule: D(f(g(x))= Dg(f(x)).Df(x) (requires param. surfaces)
as a linear map,
Jacobian as best affine approx for vector field at equilibria,
general chain rule: D(f(g(x))= Dg(f(x)).Df(x) (requires param. surfaces)