


Next: Volumes of our
Up: A Model of
Previous: A Model of
In this section of the lab, we will estimate the area enclosed by the
walls of our Metrodome model. Naturally, our answers will depend
on our mathematical model.
QUESTION 1: The crudest approximation for the stadium shape is
a rectangle.
- Set up an iterated integral for the area of the rectangle satisfying
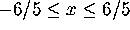 and
and 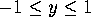 .
.
- Although the integral is trivial to solve by hand, let's gain
experience using Maple to compute
a double integral for the area:
int( int(1, y=-1..1), x=-6/5..6/5);
- Why is the integrand of the previous integral equal to 1?
QUESTION 2:
A different model for the stadium is to assume the walls of the Metrodome
are given by an ellipse with axes of length 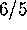 and 1.
and 1.
- Set up an iterated integral for the area of the ellipse and
compute the integral to find the are of the ellipse. Hint: to
prevent ``parenthesis mismatch,'' define
M :=
sqrt(1-(5*x/6)^2);
and use a
domain of integration that looks like
y=-M..M, x=-6/5..6/5.
- Compute the integral to find the area of the ellipse.
QUESTION 3:
A more sophisticated model postulates that the walls of the stadium satisfy
the equation

- Set up an iterated integral for the area enclosed by this curve.
- Compute the integral to find the area. Hint: Maple will be
unable to symbolically solve the integral. Use the evalf command to
evaluate the integral numerically.
QUESTION 4: As part of your lab report, comment on the models
above and how well you think they correspond to reality. We have
attached some Metrodome Facts to help you make informed decisions.
For example you may want to consider:
- What is the scale factor in this problem ( i.e., 1 unit is how
many feet)? Use this to estimate the area enclosed by the walls of
the real Metrodome.
- Do some models definitely over- or under-estimate the area? Why?



Next: Volumes of our
Up: A Model of
Previous: A Model of
Bob Hesse
Thu Feb 20 09:21:36 CST 1997
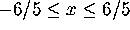 and
and 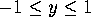 .
.
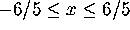 and
and 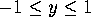 .
.
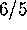 and 1.
and 1.
