You will have one week to complete this lab, professionally write up
the answers, and submit it for a grade. The purpose of the lab is
- to discover the geometry of eigenvectors of
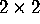 matrices
matrices - to understand relationships between eigenvalues, eigenvectors
and the determinant.
- to discover that
the determinant gives information about the way that a linear
transformation expands or contracts area.
Background:
Eigenvalues and eigenvectors play a vital role in understanding the
behavior of differential equations in the neighborhood of an equilibrium.
In this lab you will explore
the geometrical relationship between eigenvalues, eigenvectors,
and the determinant.
To get started, launch Matlab and type in the following command:
eigshow
Matlab will prompt you to type in a 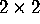 matrix. At the prompt type:
matrix. At the prompt type:
[3 3; 1 2]
This command will store the matrix
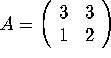 in the Matlab procedure eigshow.
Note how to enter matrices in Matlab: type the
first row (separating entries either by a space or by a comma),
then a semi-colon, then the next row, etc.
in the Matlab procedure eigshow.
Note how to enter matrices in Matlab: type the
first row (separating entries either by a space or by a comma),
then a semi-colon, then the next row, etc.
A window should appear with a white unit circle in
the center.
By holding down any mouse button and moving the mouse, you can
move the yellow radius around the circle. As you do this a blue vector will
appear
that traces out an ellipse. Think of the yellow line as a unit vector, v. Matlab is
plotting the image of that vector, Av, in blue.
Recall that an
eigenvector of a
matrix A is any non-zero vector u such that 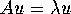 where
where 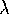 is a scalar
called the eigenvalue. Geometrically, this says u is
an eigenvector
of a matrix if its image under A is a scalar multiple of itself.
Note on your screen that Matlab shows in the lower left hand corner
the unit vector v in yellow, and in the lower right hand corner the image
of the vector, Av, in blue.
is a scalar
called the eigenvalue. Geometrically, this says u is
an eigenvector
of a matrix if its image under A is a scalar multiple of itself.
Note on your screen that Matlab shows in the lower left hand corner
the unit vector v in yellow, and in the lower right hand corner the image
of the vector, Av, in blue.
QUESTION 1: Slowly move the unit vector, v, around the unit circle.
As you do so, watch the image vector, Av.
- Approximately find two
linearly independent positions for v so that
Av is a scalar multiple of v.
(Hint: in one position, the image vector will be pointing opposite
from v.)
- For each position you find, what is the scalar that you would
multiply v by in order to get the vector Av?
- Using the proceeding answers, estimate the eigenvalues and
eigenvectors of the matrix A.
- When you write up your report,
you will know how to compute the exact eigenvalues and eigenvectors
for A. Do so, and compare the
exact values to your estimates.
As you move the vector v (in yellow) about the unit circle, its image
traces out an ellipse (in blue). In other words, the image of the
unit circle under the linear transformation represented by A is an
ellipse.
The area of an ellipse is 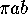 where a is the length of its
semi-major axis, and b is the length of its semi-minor axis. For our
ellipse, the semi-major axis will be the longest image vector, and the
semi-minor axis will be the shortest image vector. In the upper right
hand corner of the Figure window, Matlab displays the norm of the
vector Av. When this number is largest, you have approximately
found a semi-major axis; when it is smallest, you have found a
semi-minor axis.
where a is the length of its
semi-major axis, and b is the length of its semi-minor axis. For our
ellipse, the semi-major axis will be the longest image vector, and the
semi-minor axis will be the shortest image vector. In the upper right
hand corner of the Figure window, Matlab displays the norm of the
vector Av. When this number is largest, you have approximately
found a semi-major axis; when it is smallest, you have found a
semi-minor axis.
QUESTION 2:
- Estimate the length of the ellipse's semi-major and semi-minor
axes.
- What is the ratio of the area of the ellipse to the area of the unit circle?
- Fill out the remaining entries of Table 1 for this matrix.
Now let's change the matrix we've been studying.
To do this, type eigshow and hit return in the window from which you
started Matlab. When prompted for a new matrix,
type [1 3; 3 1]. This will create the matrix
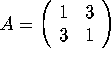 .
.
QUESTION 3: Answer the previous two questions for the new
matrix. Formulate a conjecture relating the eigenvalues
of a matrix to the way that the matrix expands or contracts area.
Let's change the matrix one more time, this time to
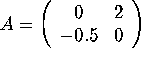 .
.
QUESTION 4:
- Why can't you use the previous procedure to find the eigenvectors
and eigenvalues for this matrix? In a paragraph, explain the
geometric relationship between v and its image, Av, as v moves around the
unit circle.
- Even for this matrix, the image of all unit vectors is
an ellipse. Compute the length of the semi-major and semi-minor axes,
and the ratio of the area of the ellipse to the area of the unit circle.
Based on your experience with the
previous two matrices, predict the remaining entries of Table 1.
Explain how you reached your conclusions.
QUESTION 5:
Compute the determinant of each matrix we've encountered in this lab.
Formulate a conjecture relating the determinant of a matrix
to its eigenvalues and to the way that the matrix transforms area.
This page is brief summary of some Matlab commands for matrices and
vectors. Although none of these commands are required to do this lab,
you are expected to know them for future labs.
About this document ...
Return to Labs Homepage
Return to Calculus 3353/3354 Homepage
URL: http://www.geom.umn.edu/~math335x/Labs/Lab09/Lab09.html
Copyright: 1996 by the Regents of the University of Minnesota.
Department of Mathematics. All rights reserved.
Comments to:
hesse@math.umn.edu
Last modified: Jan 16, 1997
The University of Minnesota is an equal opportunity educator and employer.
![]() matrix. At the prompt type:
matrix. At the prompt type: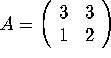 in the Matlab procedure eigshow.
Note how to enter matrices in Matlab: type the
first row (separating entries either by a space or by a comma),
then a semi-colon, then the next row, etc.
in the Matlab procedure eigshow.
Note how to enter matrices in Matlab: type the
first row (separating entries either by a space or by a comma),
then a semi-colon, then the next row, etc.
![]() where
where ![]() is a scalar
called the eigenvalue. Geometrically, this says u is
an eigenvector
of a matrix if its image under A is a scalar multiple of itself.
Note on your screen that Matlab shows in the lower left hand corner
the unit vector v in yellow, and in the lower right hand corner the image
of the vector, Av, in blue.
is a scalar
called the eigenvalue. Geometrically, this says u is
an eigenvector
of a matrix if its image under A is a scalar multiple of itself.
Note on your screen that Matlab shows in the lower left hand corner
the unit vector v in yellow, and in the lower right hand corner the image
of the vector, Av, in blue.
![]() where a is the length of its
semi-major axis, and b is the length of its semi-minor axis. For our
ellipse, the semi-major axis will be the longest image vector, and the
semi-minor axis will be the shortest image vector. In the upper right
hand corner of the Figure window, Matlab displays the norm of the
vector Av. When this number is largest, you have approximately
found a semi-major axis; when it is smallest, you have found a
semi-minor axis.
where a is the length of its
semi-major axis, and b is the length of its semi-minor axis. For our
ellipse, the semi-major axis will be the longest image vector, and the
semi-minor axis will be the shortest image vector. In the upper right
hand corner of the Figure window, Matlab displays the norm of the
vector Av. When this number is largest, you have approximately
found a semi-major axis; when it is smallest, you have found a
semi-minor axis.
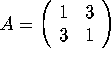 .
.
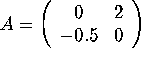 .
.