This worksheet does not need to be handed in, but you are responsible
for the material.
The purpose of the lab is to understand how to completely understand
the qualitative phase portraits of linear vector fields.
(Intuitively, we say that two differential equations are qualitatively
similar if their phase portraits look the same.) As we saw in
a previous lab, this means that we can understand the local
behavior of most vector fields near equilibria.
In a previous lab we saw that if (p, q) is a ``typical'' equilibrium of a
vector field defined by 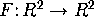 , then
, then
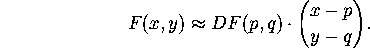
In words, the equation above says that near a typical equilibrium,
vector fields ``look'' like linear vector fields, so in this lab
we will classify the appearance of most linear vector fields.
For convenience, we will choose the equilibrium point to be at the
origin, (p,q)=(0,0). Then the
matrix
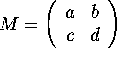 is the coefficient matrix for the linear vector field
is the coefficient matrix for the linear vector field
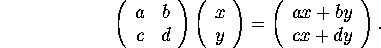
Recall that the determinant of the above matrix is

and the trace of the matrix is

To start this lab, launch Matlab and pplane.
Choose the ``linear system'' example from pplane's gallery of
pre-defined differential equations. (Note that pplane
uses capital letters for its matrix parameters.)
ACTIVITY 1: Centers
The phase portraits you will see in this section of the lab are called
centers.
Change the values of the coefficient matrix to
(a,b,c,d)= (0,1,-0.5,0) so that we may study the phase portrait of
the differential equation

- Compute a phase portrait for the linear system given above.
- Compute the trace and determinant of the matrix M
for the specific values of coefficients (a,b,c,d) used above.
- Plot the ordered pair
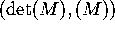 on the diagram provided.
on the diagram provided. - Next to the ordered pair you just plotted, sketch the phase portrait
of the linear ODE associated with this matrix. [This has been done
for you!]
Put arrows on the phase portrait to indicate the direction that trajectories
flow.
- Clear the old phase portrait. Change the entries of M
to (a,b,c,d)=(0,1,-0.125,0). Repeat the
steps specified above to plot the trace and determinant on
the supplied diagram, and to sketch the phase portrait of the associated
linear ODE.
ACTIVITY 2: Foci
The phase portraits you will see in this section of the lab are called
foci. The equilibrium in the phase portrait for a focus is sometimes referred
to as a ``sink'' (when nearby orbits are attracted to it) or a ``source''
(when nearby orbits are repelled by it).
- Clear the old phase portrait.
Compute a phase portrait to the linear differential equation
determined by the matrix with entries (a,b,c,d)=(-1,1,-0.5,0).
- Compute the trace and determinant of the associated matrix M.
- Again, plot the ordered pair
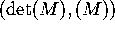 on the diagram provided.
Sketch the phase portrait on the diagram and put
arrows on the phase portrait to indicate the direction that trajectories
flow.
on the diagram provided.
Sketch the phase portrait on the diagram and put
arrows on the phase portrait to indicate the direction that trajectories
flow. - Clear the old phase portrait and do
the same activity for the linear differential equation determined by
the matrix with entries (a,b,c,d)=(1,1,-0.5,0).
ACTIVITY 3: Nodes
The phase portraits you will see in this section of the lab are called
nodes. As was the case for the focus equilibria, the equilibrium in the phase
portrait for a node is referred to as a ``sink'' or a ``source,'' depending on
whether or not it is locally attracting.
- Clear the old phase portrait.
Compute the phase portrait for
the linear differential equation determined by the matrix
with entries (a,b,c,d)=(-1,1,-0.125,0).
- Compute the trace and determinant of the associated matrix.
- Plot the ordered pair
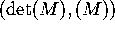 on the diagram provided, and
sketch the phase portrait (with arrows!) on the diagram.
on the diagram provided, and
sketch the phase portrait (with arrows!) on the diagram. - Do the same for the linear differential equation determined by the
matrix with entries (a,b,c,d)=(1,1,-0.125,0).
ACTIVITY 4: Saddles
The phase portraits you will see in this section of the lab are called
saddles. They are characterized by having one direction in which trajectories
are attracted to the equilibrium, and another direction in which trajectories
move away from the equilibrium.
- Compute solutions to the linear differential equation determined by the
matrix with entries (a,b,c,d)=(1,1,0.5,0). Enter the usual
information on the supplied diagram.
- Do the same for the linear differential equation determined by the
matrix with entries
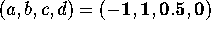 .
.
ACTIVITY 5:
In your group, choose three random 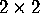 matrices. Compute their
trace and determinant. Using your previous work,
predict what the phase portrait will
look like before you compute it.
matrices. Compute their
trace and determinant. Using your previous work,
predict what the phase portrait will
look like before you compute it.
ACTIVITY 6:
The trace and determinant almost (but not quite!) completely determine
the dynamics of a linear differential equation. Choose one of the matrices
that we investigated. Find a different matrix that has the same
trace and determinant but which has different dynamics. For example, one the
phase portrait might wind in the clockwise direction, whereas the other winds
counterclockwise.
ACTIVITY 7:
Create a coefficient matrix and plot the linear phase portrait for
a linear system whose coefficient
matrix satisfies
-
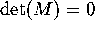 ,
, 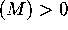
-
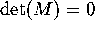 ,
, 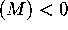
-
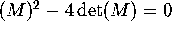
In what ways might these phase portraits be considered ``degenerate''
or ``atypical''? (Hint: For the last phase portrait, think about the
way phase portraits ``evolve'' from a foci to a node.)
Figure: Classifying linear phase portraits
according to their determinant and trace.
About this document ...
Return to Labs Homepage
Return to Calculus 3353/3354 Homepage
URL: http://www.geom.umn.edu/~math335x/Labs/Lab08/Lab08.html
Copyright: 1996 by the Regents of the University of Minnesota.
Department of Mathematics. All rights reserved.
Comments to:
hesse@math.umn.edu
Last modified: Jan 15, 1997
The University of Minnesota is an equal opportunity educator and employer.
![]() , then
, then
![]()
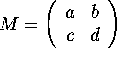 is the coefficient matrix for the linear vector field
is the coefficient matrix for the linear vector field
![]()
![]()
![]()
![]()