This worksheet does not need to be handed in, but you are responsible
for the material.
The purpose of the lab is to explore the idea that
linear vector fields can approximate nonlinear vector fields, and that
this approximation is particularly useful near
an equilibrium point.
We know that if F is a differentiable function of two variables, then
the function F is well-approximated near the point (p, q) by the
affine function 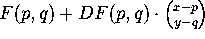 .
(Affine just means ``linear plus a constant term''.)
.
(Affine just means ``linear plus a constant term''.)
Note that if 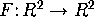 is a vector field, and if
(p,q) is an equilibrium, then F(p,q) is the zero vector
(why!). Then near a ``typical'' equilibrium,
is a vector field, and if
(p,q) is an equilibrium, then F(p,q) is the zero vector
(why!). Then near a ``typical'' equilibrium,
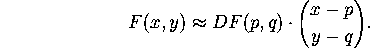
Remark: The word ``typical'' is used to eliminate cases where, for example,
DF(p,q) might be the zero matrix. A ``non-typical'' equilibrium
might be, for example, a critical point of a gradient vector field at
which the second derivative test fails to classify the equilibrium as
a min/max/saddle.
In words, the equation above says that near a typical equilibrium,
vector fields ``look'' like linear vector fields! We have already seen in
an earlier lab that AWAY from equilibria, vector fields look
constant, so this lab will focus
on approximations near equilibria. (To be honest, the vector fields
we will consider in this lab are ``affine'' rather than linear, but
they can be made linear by a simple change of coordinates, so we will
sometimes
continue to use the slightly inappropriate term ``linear'' to refer to
vector fields that contain only first powers of the variables.)
In this lab we will study the pendulum differential equation
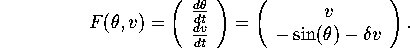
The variable 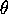 measures the angle of the pendulum bob, using
``straight down'' to be
measures the angle of the pendulum bob, using
``straight down'' to be 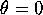 . In particular, the pendulum is
straight up when
. In particular, the pendulum is
straight up when 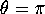 (or
(or 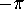 ).
The variable v is an angular
velocity. The parameter
).
The variable v is an angular
velocity. The parameter 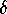 is a ``dissipation'' (or damping) parameter:
is a ``dissipation'' (or damping) parameter:
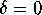 gives us a Hamiltonian differential equation whose
solutions run along level sets of the Hamiltonian function (a.k.a,
``the energy surface''), whereas
gives us a Hamiltonian differential equation whose
solutions run along level sets of the Hamiltonian function (a.k.a,
``the energy surface''), whereas 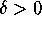 is the physically
realistic case in which the pendulum encounters resistance from the
surrounding medium, and so
loses energy.
is the physically
realistic case in which the pendulum encounters resistance from the
surrounding medium, and so
loses energy.
To get started,
prior to
launching Matlab and pplane.
Choose the ``pendulum'' example from pplane's gallery of
pre-defined differential equations. (Note that pplane
uses D instead of 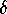 as a dissipation parameter; we will
reserve D to mean the ``Jacobian operator.'')
as a dissipation parameter; we will
reserve D to mean the ``Jacobian operator.'')
ACTIVITY 1:
Set the display domain to 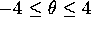 ,
, 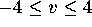 and generate a phase portrait for the pendulum equation with
and generate a phase portrait for the pendulum equation with
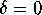 .
There are two equilibria: one a center at
.
There are two equilibria: one a center at 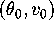 , and the other a
saddle at
, and the other a
saddle at 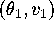 .
Analytically locate the two equilibria (that is, find the values of
.
Analytically locate the two equilibria (that is, find the values of
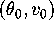 and
and 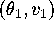 )
and compute the Jacobian of the vector
field evaluated at each equilibrium. Write down the evaluated
Jacobian for later reference.
)
and compute the Jacobian of the vector
field evaluated at each equilibrium. Write down the evaluated
Jacobian for later reference.
ACTIVITY 2:
Make sure 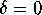 . Clear all trajectories.
For EACH of the two equilibria you found:
. Clear all trajectories.
For EACH of the two equilibria you found:
- Use pplane to numerically locate the equilibrium.
- Zoom in to a region of ``radius 1/2'' about the
equilibrium. That is, the display window should show
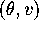 values for which
values for which 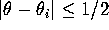 and
and 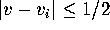 , i=0,1.
, i=0,1. - Generate a ``local phase portrait'' of the pendulum
near each equilibrium.
(Hint: For easy comparison with later phase portraits, try to
choose initial conditions that are reproducible. For example,
you might choose initial conditions spaced uniformly along the boundary
of the display window.)
- Print out this local phase portrait. (Hint: to easily distinguish your
printouts, investigate the
item under the PPLANE Options menu that enables you to ``Enter
text on the Display Window.'' You will have to type the text into the
shell window from which you launched matlab. Include the fact
that
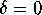 on the printout.)
on the printout.)
ACTIVITY 3:
Choose a value of 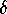 from the
set
from the
set 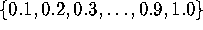 .
Reset the domain to
.
Reset the domain to 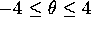 and
and 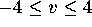 and generate a phase portrait for the pendulum equation, now with
and generate a phase portrait for the pendulum equation, now with
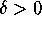 .
Again, there are two equilibria: let the stable equilibrium be at
.
Again, there are two equilibria: let the stable equilibrium be at
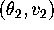 .
Analytically locate the position of the stable equilibrium
and compute (and record) the Jacobian of the vector
field evaluated at
.
Analytically locate the position of the stable equilibrium
and compute (and record) the Jacobian of the vector
field evaluated at 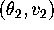 .
.
Repeat Activity 2 to generate a local phase
portrait near 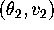 . Include your value of
. Include your value of
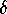 on the printout.
on the printout.
At this point you have three local phase portraits. You also have three
matrices that represent the affine vector
fields that best approximate the vector field of the pendulum near
each equilibrium. How do these matrices give rise to an affine
vector field, and how well does that vector field approximate the phase
portraits we've computed?
For a matrix
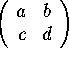 ,
the matrix generates affine vector fields of the form
,
the matrix generates affine vector fields of the form
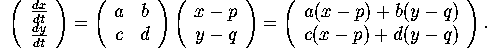
In practice, the constants (p,q) are often the position of an
equilibrium, and the matrix is obtained by evaluating the Jacobian at that
equilibrium.
Choose the ``linear system'' example from pplane's gallery of
pre-defined differential equations. (Note that pplane
uses capital letters for its matrix parameters.)
ACTIVITY 4:
For each pendulum equilibrium, 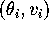 , i=0,1,2,
set the domain of the display window to the same domain values
you used in Activities 3 and 4 when you generated local phase
portraits of the pendulum.
, i=0,1,2,
set the domain of the display window to the same domain values
you used in Activities 3 and 4 when you generated local phase
portraits of the pendulum.
For each i=0,1,2:
- Input the coefficients of
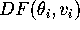 into pplane. (You may need to add a constant to
the equations that define the linear vector field.)
into pplane. (You may need to add a constant to
the equations that define the linear vector field.) - Generate a phase portrait for the affine
system defined by the matrix
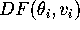 .
. - Print out the linear phase
portrait and superimpose it onto the corresponding local
phase portrait of the pendulum equation. (For example, place one sheet
of paper over the other and hold them up to the light.)
Question: Does the affine vector field approximate the pendulum
field near equilibria? How well? How could you make the approximation
better?
Near a saddle equilibrium, there are trajectories that asymptotically
approach/leave the equilibrium. These may be numerically found in
pplane by locating the equilibria, and then choosing the item
labeled ``Plot stable and unstable orbits'' under the PPLANE
Options menu. Four distinct trajectories approach the
equilibria, so that the phase portrait locally looks like an ``X''.
We will call any of these four special trajectories a separatrix
(the plural form is separatrices). In other words, a separatrix
is a trajectory that asymptotically approaches a saddle equilibrium
as 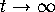 or as
or as 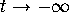 .
.
Remark: if the vector field is linear, then the separatrices really do
form an ``X,'' but as you will see from the pendulum equation, in
general the separatrices may be curves that are not straight!
ACTIVITY 5: Return to
the pendulum equation with 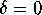 . Compute the separatrices. Zoom in near the
saddle until the separatrices look like straight lines, then graphically
estimate the slope of the separatrices as they approach
the saddle point.
. Compute the separatrices. Zoom in near the
saddle until the separatrices look like straight lines, then graphically
estimate the slope of the separatrices as they approach
the saddle point.
Now switch to the linear vector field that best approximates the
pendulum field near the saddle point. Find the separatrices of the
linear vector field and estimate the slope of those curves.
What is the relationship between the slopes of the linear and
nonlinear separatrices?
If we restrict ourselves to consider affine vector fields, then
separatrices are the images of lines that approach the equilibrium.
Geometrically, consider the vector, u, from the equilibrium
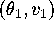 to a point
to a point 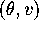 ON A SEPARATRIX near
the equilibrium. In symbols,
ON A SEPARATRIX near
the equilibrium. In symbols, 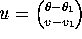 . Note that u points along the (straight) separatrix. Since
. Note that u points along the (straight) separatrix. Since
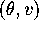 is on a separatrix, the vector field at
is on a separatrix, the vector field at 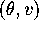 either points in the same direction as u, or else it points in the
opposite direction.
either points in the same direction as u, or else it points in the
opposite direction.
Said another way, the vector u is a scalar multiple of the vector
field at 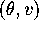 . In symbols, if
. In symbols, if
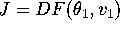 , the vector field is just the
matrix-vector product J u. If
, the vector field is just the
matrix-vector product J u. If 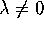 is an arbitrary scalar,
then the requirement that u is a scalar multiple of the vector
field, says that u satisfies the equation
is an arbitrary scalar,
then the requirement that u is a scalar multiple of the vector
field, says that u satisfies the equation

This equation is extremely important in higher mathematics. Vectors
u that satisfy the equation are called eigenvectors; the
constant 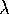 is called an eigenvalue.
We will learn more about eigenvalues and eigenvectors next quarter.
is called an eigenvalue.
We will learn more about eigenvalues and eigenvectors next quarter.
ACTIVITY 6: On your printout of the phase portrait of the linear
vector field with a saddle equilibrium,
sketch the geometry described in the previous paragraphs.
About this document ...
Return to Labs Homepage
Return to Calculus 3353/3354 Homepage
URL: http://www.geom.umn.edu/~math335x/Labs/Lab07/Lab07.html
Copyright: 1996 by the Regents of the University of Minnesota.
Department of Mathematics. All rights reserved.
Comments to:
hesse@math.umn.edu
Last modified: Jan 15, 1997
The University of Minnesota is an equal opportunity educator and employer.
![]() .
(Affine just means ``linear plus a constant term''.)
.
(Affine just means ``linear plus a constant term''.)
![]() is a vector field, and if
(p,q) is an equilibrium, then F(p,q) is the zero vector
(why!). Then near a ``typical'' equilibrium,
is a vector field, and if
(p,q) is an equilibrium, then F(p,q) is the zero vector
(why!). Then near a ``typical'' equilibrium,
![]()
![]()
![]() measures the angle of the pendulum bob, using
``straight down'' to be
measures the angle of the pendulum bob, using
``straight down'' to be ![]() . In particular, the pendulum is
straight up when
. In particular, the pendulum is
straight up when ![]() (or
(or ![]() ).
The variable v is an angular
velocity. The parameter
).
The variable v is an angular
velocity. The parameter ![]() is a ``dissipation'' (or damping) parameter:
is a ``dissipation'' (or damping) parameter:
![]() gives us a Hamiltonian differential equation whose
solutions run along level sets of the Hamiltonian function (a.k.a,
``the energy surface''), whereas
gives us a Hamiltonian differential equation whose
solutions run along level sets of the Hamiltonian function (a.k.a,
``the energy surface''), whereas ![]() is the physically
realistic case in which the pendulum encounters resistance from the
surrounding medium, and so
loses energy.
is the physically
realistic case in which the pendulum encounters resistance from the
surrounding medium, and so
loses energy.
![]() . Include your value of
. Include your value of
![]() on the printout.
on the printout.
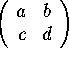 ,
the matrix generates affine vector fields of the form
,
the matrix generates affine vector fields of the form
![]()
![]() . In symbols, if
. In symbols, if
![]() , the vector field is just the
matrix-vector product J u. If
, the vector field is just the
matrix-vector product J u. If ![]() is an arbitrary scalar,
then the requirement that u is a scalar multiple of the vector
field, says that u satisfies the equation
is an arbitrary scalar,
then the requirement that u is a scalar multiple of the vector
field, says that u satisfies the equation
![]()
![]() is called an eigenvalue.
We will learn more about eigenvalues and eigenvectors next quarter.
is called an eigenvalue.
We will learn more about eigenvalues and eigenvectors next quarter.