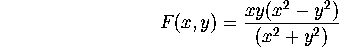
This worksheet does not need to be handed in, but you are responsible for the material. The purpose of the lab is to explore the concepts of limits, continuity, and differentiability in multivariable functions.
Geometrically, a function of two variables is differentiable at a point if its graph looks like a plane when you zoom in close enough. Said another way, a differentiable function is well-approximated near that point by a linear function (whose graph is the plane that best fits the graph of the function). Most of the functions we study in calculus are ``nice'', meaning they are continuous, and often differentiable as well. In this lab we examine some functions that are not so nice.
We will study the function
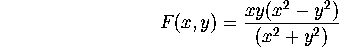
To get started, launch Maple, type
with(plots): with(linalg):,
and define F as above.
We will use Maple to geometrically test the
differentiability of F at the point 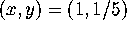 .
.
 small enough so that the graph of F over the
rectangle x=1-epsilon..1+epsilon, y=1/5-epsilon..1/5+epsilon
looks like a plane. (Use the ``Constrained'' projection.) Print out a
copy of this plot, and indicate on the plot the value you
used for
small enough so that the graph of F over the
rectangle x=1-epsilon..1+epsilon, y=1/5-epsilon..1/5+epsilon
looks like a plane. (Use the ``Constrained'' projection.) Print out a
copy of this plot, and indicate on the plot the value you
used for  .
.
Use your plot of the graph of F to estimate 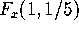 and
and
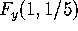 . Discuss how you can use the
geometric information from the graph of F to determine your estimates.
Now symbolically compute the actual value of the two
quantities you estimated above and compare them with your estimates.
. Discuss how you can use the
geometric information from the graph of F to determine your estimates.
Now symbolically compute the actual value of the two
quantities you estimated above and compare them with your estimates.
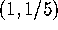 gives evidence
to the fact that F is differentiable at
gives evidence
to the fact that F is differentiable at 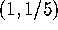 . For the rest
of the lab we will investigate the differentiability of the function
G defined by
. For the rest
of the lab we will investigate the differentiability of the function
G defined by

In fact, we will show that G is not
differentiable at 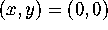 .
.
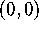 . In
other words, zoom in on the graph of G around the point
. In
other words, zoom in on the graph of G around the point 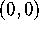 ,
picking smaller and smaller
,
picking smaller and smaller  -rectangles (again, it's
important to use the ``Constrained'' option to observe things at the
correct scale).
-rectangles (again, it's
important to use the ``Constrained'' option to observe things at the
correct scale).
What phenomenon do you observe? Explain how this
indicates that G can not be differentiable at 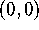 . (You do
not need to print these plots.)
. (You do
not need to print these plots.)
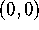 !
!
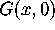 and
and 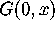 and compute the
derivatives of these one-variable functions at zero. Why does this approach
verify the existence of
and compute the
derivatives of these one-variable functions at zero. Why does this approach
verify the existence of 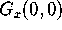 and
and
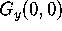 ?
?
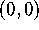 to write down
tangent vectors to the graph of G at
to write down
tangent vectors to the graph of G at 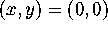 in the coordinate
directions.
in the coordinate
directions.
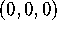 and spanned
by the tangent vectors you computed above, and graphically display
this plane together with the graph of G on the
domain x=-1..1, y=-1..1. Print out a copy of this plot.
and spanned
by the tangent vectors you computed above, and graphically display
this plane together with the graph of G on the
domain x=-1..1, y=-1..1. Print out a copy of this plot.
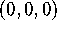 do not lie in the plane you computed above!
do not lie in the plane you computed above!
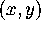 -plane
for which the tangent vector does
not seem to lie in the plane spanned by tangent vectors in the coordinate
directions. Parametrize a line in this direction and
evaluate G along
this line. ( Hint: All non-vertical lines passing through the
origin are of the form y=mx and their parametrizations in the
x,y-plane are therefore
-plane
for which the tangent vector does
not seem to lie in the plane spanned by tangent vectors in the coordinate
directions. Parametrize a line in this direction and
evaluate G along
this line. ( Hint: All non-vertical lines passing through the
origin are of the form y=mx and their parametrizations in the
x,y-plane are therefore 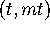 .)
.)
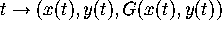 does not lie
in the plane found in the previous activity.
does not lie
in the plane found in the previous activity.
 ?
?
There is a theorem (p. 181) that says that G
must be differentiable if the partial derivatives for G exist
and are continuous. We've just shown that the partial derivatives for
G exist at 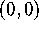 and that G is not differentiable there.
So at least one of the partial derivatives of G must not be
continuous at
and that G is not differentiable there.
So at least one of the partial derivatives of G must not be
continuous at 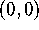 . (If you follow this logic, consider
going into mathematics.)
. (If you follow this logic, consider
going into mathematics.)
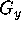 on the domain
x=-1..1, y=-1..1. Use the plot to show graphically why this new function
is not continuous at
on the domain
x=-1..1, y=-1..1. Use the plot to show graphically why this new function
is not continuous at 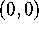 .
.
( Hint: To be continuous, the limit must be the same from any
direction. Be careful of what Maple is showing you---technically the
partial derivatives of G are not defined at 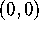 , so Maple tries
to ``sew up'' everything there. You should concentrate on the behavior
of the graph outside of this messy area.)
, so Maple tries
to ``sew up'' everything there. You should concentrate on the behavior
of the graph outside of this messy area.)
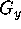 ) the discontinuity you observed above.
) the discontinuity you observed above.