Lab #3

Each group should professionally write up the answers to this lab and hand it in.

The purpose of the lab is

1. to use technology to visualize surfaces in space;
2. to understand how surfaces are built by one-parameter families of one-dimensional curves;
3. to compute tangent vectors to a surface in the direction of a coordinate axis, and understand the geometric meaning of these vectors;
4. to discover the ``tangent plane'' to a surface as the span of linearly-independent tangent vectors.

Log in to your account and launch Maple. The first command you should type into Maple is
with(linalg): with(plots):
which will enable you to use a host of Maple plotting commands.

In this lab, we will exclusively study the graph of the function

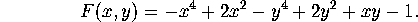
To make your life easier, define this expression in Maple by
F := -x^4 + 2*x^2 - y^4 + 2*y^2 + x*y - 1;
and visualize the graph of this function near the origin by
plot3d( F, x=-1.6..1.6, y=-1.6..1.6);
Use the menu-bar on the plot window to add ``Boxed'' axes to your graph. Also, color-code the function by its height and display the surface as a ``Patch and Contour'' plot.

1. If we intersect the graph of F with the vertical plane y=1, we will get a function of one variable. You can think of this function as g(x) = F(x,1).
   1. Explicitly write out this single-variable function.
   2. Plot or sketch the graph of g. How does the graph of this one-variable function relate to the graph of F?
   3. What are the critical points of g? How do they relate to geometric features on the graph of F?
   4. Parametrize the tangent line to g at the point x=1/2. Hint: The line passes through the point (1/2, g(1/2)). [Note: it is tempting to represent the tangent line as the graph of a function, but we want the tangent line to be parametrized.]
   5. Test your computation by using Maple's plot command to represent the tangent line and the graph of g on the same plot. (Hint: recall that you can think of the graph of g as a parametrized image by considering 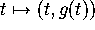. Look on your Maple summary sheet to see how to display two parametrized curves on the same plot.) Print out this Maple plot and include it in your lab report.
   6. How does the derivative of g relate to a partial derivative of F? Using this connection, find a tangent vector to the graph of F in the x-direction at the point (1/2,1,F(1/2,1)).
2. Define h(y)=F(1/2,y) to be the single-variable function obtained by restricting the domain of F to the line x=1/2? Answer the previous questions for h. In particular
   1. Determine the relationship between the graph of h and the graph of F.
   2. Parametrize the tangent line to h at the point y=1.
   3. Plot the graph of h and its tangent line at (1,h(1)).
   4. Find a tangent vector to the graph of F in the y-direction at the point (1/2,1,F(1/2,1)).
3. We now have a point, (1/2,1,F(1/2,1)), on the surface and two vectors that are tangent to the surface. If the tangent vectors are linearly independent, then they span a plane. We will call such a plane a tangent plane.
   1. Verify that one tangent vectors is not a multiple of the other, and therefore conclude that the tangent vectors are linearly independent.
   2. The tangent plane is therefore the span of these two vectors. If 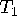and 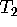are the two tangent vectors, then the tangent plane is parametrized by

      

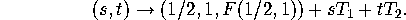
      Write out each component of the function that parametrizes the tangent plane and verify your answer by using Maple's plot3d command to simultaneously plot the tangent plane and the graph of F. (Hint: parametrize the graph of F as 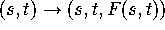.) Submit this plot with your lab writeup.

About this document ...
Return to Labs Homepage
Return to Calculus 3353/3354 Homepage URL: http://www.geom.umn.edu/~math335x/Labs/Lab03/Lab03.html
Copyright: 1996 by the Regents of the University of Minnesota.
Department of Mathematics. All rights reserved.
Comments to: hesse@math.umn.edu
Last modified: Oct 23 1996
The University of Minnesota is an equal opportunity educator and employer.