Basic Maple Syntax

?

Typing a question mark followed by a mathematical term will often generate help on the associated Maple command. For example, ?integrate brings up the help page associated with integration.

Colon and Semicolon

All Maple statements must be terminated by a semicolon (;) or a colon (:). Maple will not execute a statement unless it is terminated by a semicolon or colon. Usually you should end a statement with a semicolon. If you use a colon, the Maple output from the statement is suppressed. This may be useful if the output is long or is only one step along the way to an answer. For example, 2^18; is an output you might want to see, but you probably want to supress the output for int( 1/(x^50*sqrt(3+x)), x);

Double Quotes

The double quote operator (") recalls the most recent output in a Maple session. This can be used to enter the output into a command. Two double quotes ("") refers to the second most previous result and three double quotes (""") to the third most previous output. In general however, if you have an output that you will want to use again in the Maple session it is better to assign that output to a variable name (see the description below) so it can be recalled later in the session.

Arithmetic Operations

Maple uses the standard arithmetic operations, +, -, *, and / for addition, subtraction, multiplication and division, ^ for exponentiation and ! for factorial. The order in which operations are executed follow the standard mathematical rules. If there are any ambiguities, uses parentheses.

Entering a range of values

The expression x = a..b denotes x in the interval 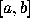. This can be used to enter a domain or range in a plot command or endpoints of integration for a definite integral in the int command as well as in other contexts.

Maple commands

Maple commands are called using the syntax

commandname(parameter1, parameter2, . . .);

Maple is case-sensitive so it is important to be careful when entering the command name. The parameters for the command can be Maple expressions, numbers, other Maple commands or previously generated Maple output. If you are uncertain about a particular command, you should use the Help Browser or Keyword search to determine the appropriate usage of the command.

Loading Packages

Not all Maple commands are immediately accessible. Some commands are found in specialized packages such as linalg, plots, etc. These packages can be loaded with the command with(packagename):. After the package is loaded, any command in the package can be accessed as above. For example, we will often type with(plots): with(linalg):

---

QUESTION 1: Load the plots and linalg packages. What ``warnings'' does Maple give? (This is normal behavior.)

---

Assignment operator

The := operator can be used to assign a Maple expression to a variable name. This expression could be anything from a constant to the output of a Maple command. This is particularly useful if the output will be used in subsequent Maple commands. For example, the command

r:= 5;

assigns the value 5 to the variable r. The command

area:= int(1/x, x = 1..3);

computes the definite integral 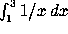and assigns that value to a variable.

In order to unassign a previously assigned variable use a command like

r:= 'r';

Note that these quotation marks are the ``forward apostrophe.''

Defining Functions

The syntax for defining functions in Maple uses the assignment operator := and the symbol -> which is built up from - and >. For example to define 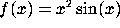enter

h:= x -> x^2*sin(x);

To define 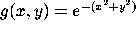enter

g:= (x,y) -> exp(-(x^2 + y^2));

After these functions have been defined, they can be evaluated at a point or used in a subsequent Maple command. For example h(1) or g(-1,2) are valid commands and yield numbers.

A function is different than an expression:

f:= x^2*sin(x);

is a valid assignment, but the expression f(Pi) does NOT make sense because f is not a function. If you want the value of the expression at 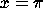, try subs( x=Pi, f );.

Constants

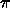The Maple constants we will use are Pi for and E for e (the base of the natural logarithm).