S(r,h) = 4 Pi r^2 + 2 Pi r hand the volume of the tank is
V(r,h) = 4 Pi/3 r^3 + Pi r^2 h.Then if lambda is a Lagrange multiplier, the solution will occur for values of (r,h,lambda) where
grad(S) = lambda grad(V)
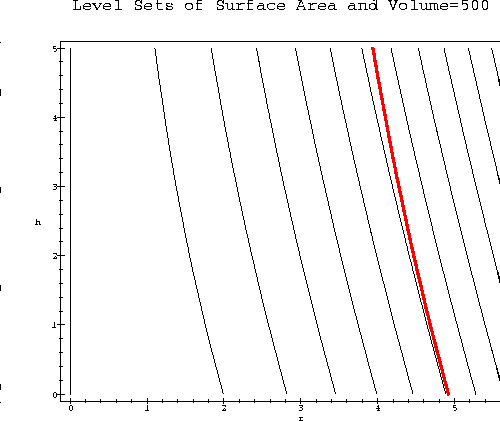
V(r,h) = 500.
Solving these equations simultaneously, we find that the minimum surface area occurs when (r,h)=( (375/Pi)^(1/3), 0).
You asked me to investigate the problem of building a cylindrical storage tank that holds 500 cubic meters of liquid. In an attempt to minimize our production costs, I attempted to design a tank that requires the least possible surface area.
The problem of minimizing some function (like our surface area) while satisfying some constraint (such as a constant volume) is a standard problem in multivariable calculus. The usual approach is the so-called "Method of Lagrange Multipliers." I can supply the details if need be, but perhaps it is sufficient to note that this method allows us to look for the radius and length of a tank that has the least surface area. The general idea is to stay on a curve corresponding to the volume constraint, and look for maximum and minimum values of the cost function along this curve.
Upon completing my analysis, I was surprised to find that the tank that minimizes surface area would be a spherical tank of radius 4.92 meters. Unfortunately, our customer explicitly specified a cylindrical tank. I recommend contacting the customer to
- Inform them of this least cost solution;
- Determine whether this solution is acceptable for their needs;
- If a sphere is unacceptable, determine the smallest length that they will accept for the cylindrical "middle" of their tank. This is the length that will be least expensive to build, while still conforming to the customer's needs.
Sincerely,
P. Lagrange