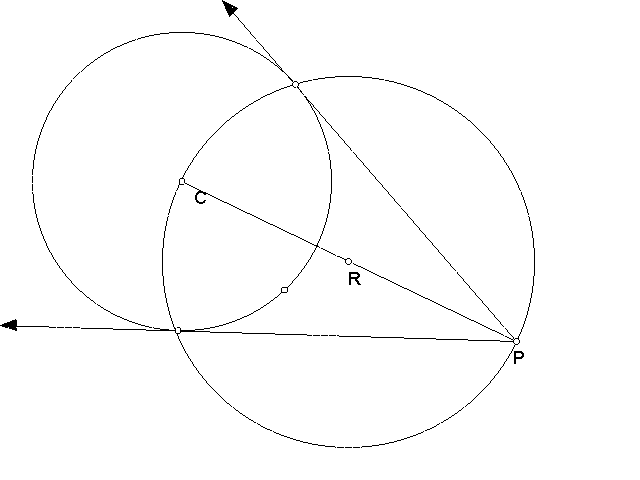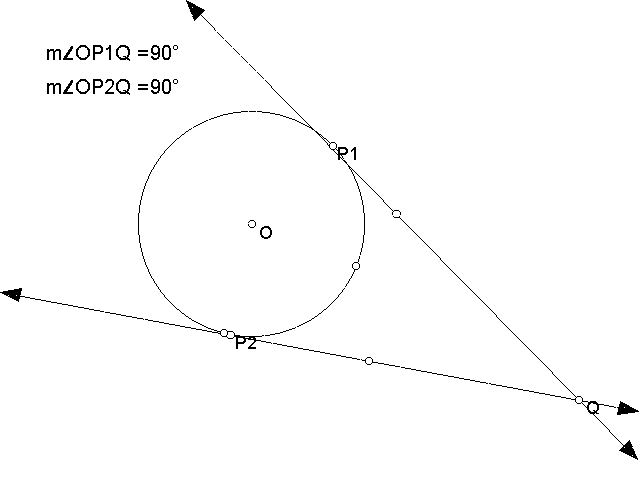
1. The math fact is that the tangent line and the raduis line to the tangent point are perendicular.

2. The math fact is that parallel diameters intersect circles at points that are collinear with the center of symetry of the two circles

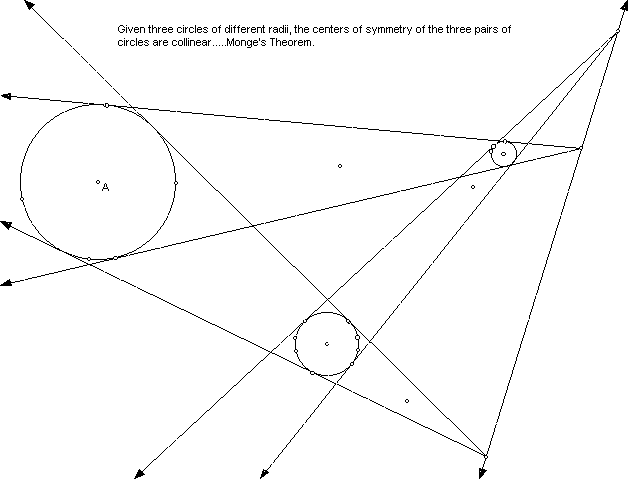
3. Given three circles of different radii, the centers of symmetry of the three circles are collinear.

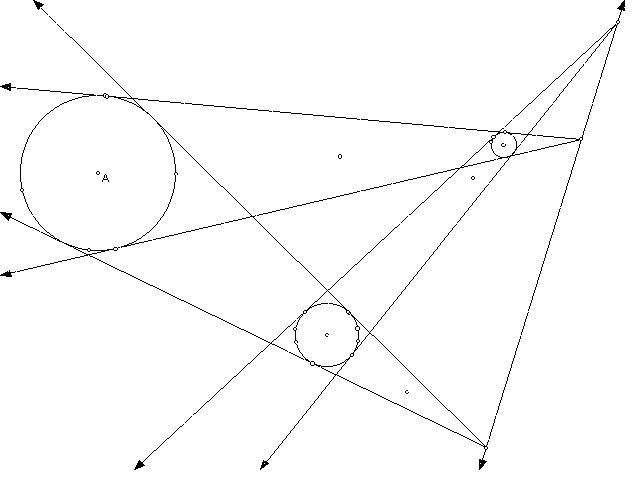here

4.

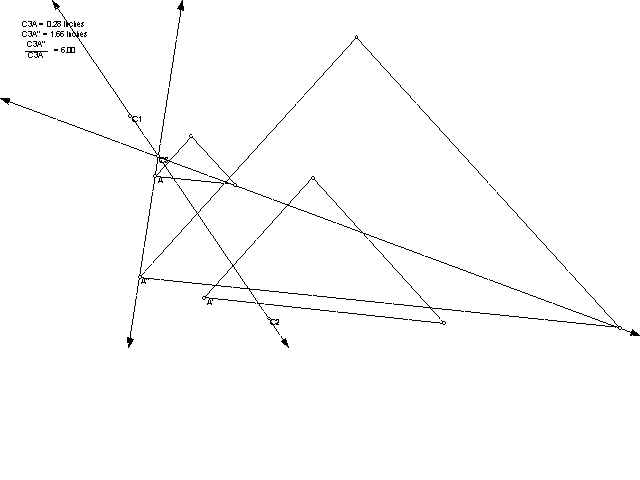
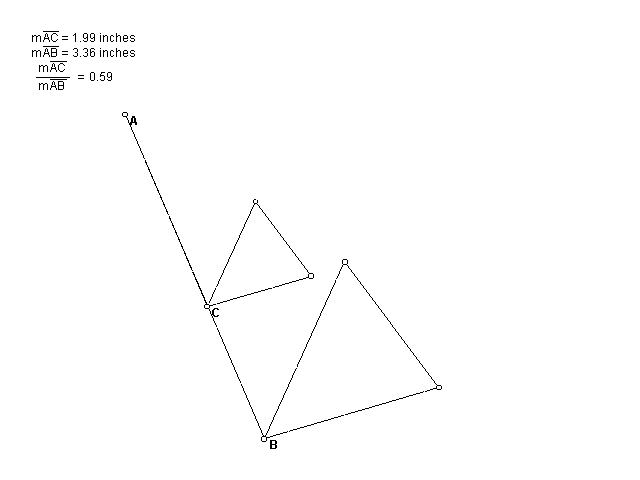
5. The composition of two dilations is itself a dialation.

The center of dilation for circles is the point at which the tangent lines for the two circles meet. The line connecting the centers of the circles will pass through this center also, just as it is a point to be dilated by the ratio. If the ratio of dilation is 1, the figure is translated and there will be no common center of dilation. A ratio product of 1 produces points that form parallel lines, hence no intersection.

A third center of dilation is collinear to the previous two centers when making a composition of dilations. Two tangent lines intersect at a center. Tangent intersections are points of centers and are in fact collinear.

6. See Kristine's web page as linked to above.

click here.

TANGENT TO A CIRCLE?

How would you construct a tangent line to a circle, going through a point outside the circle, using only a straight-edge and compass? Lets try it together.

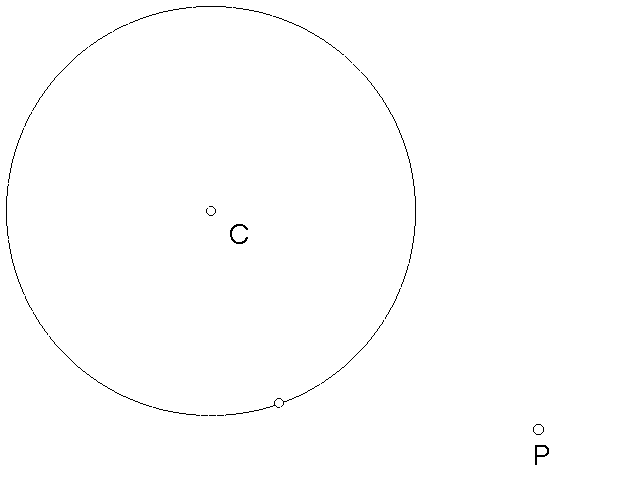
Step one: Using the compass, make a circle and label the center C.

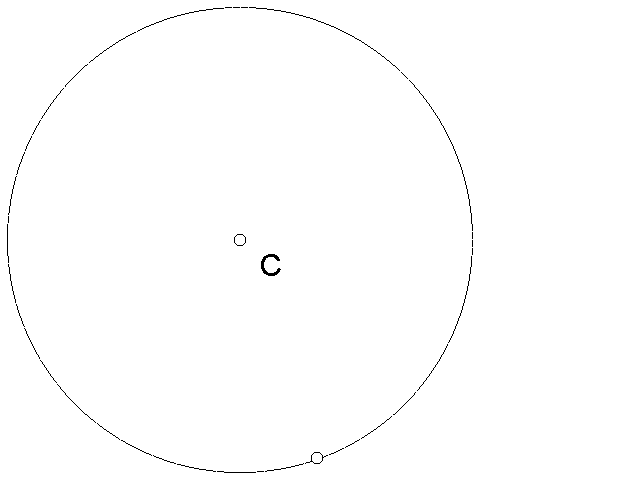
Step two: Pick any point outside of the circle, label it P.

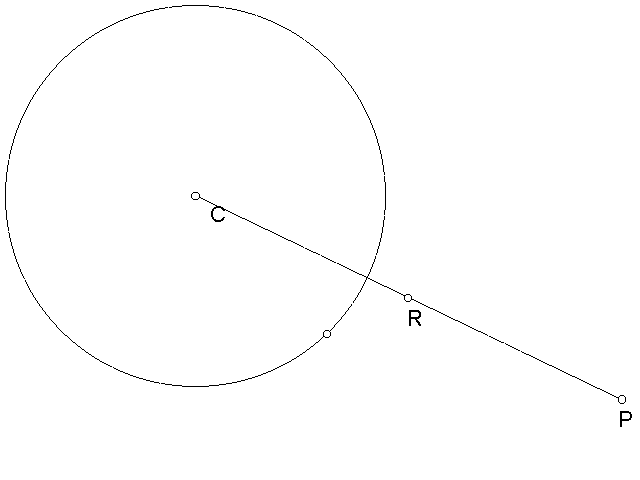
Step three: Make a line segment from P to C. Find and label midpoint R.

Step Four: Construct a circle with center R and a radius of RP.

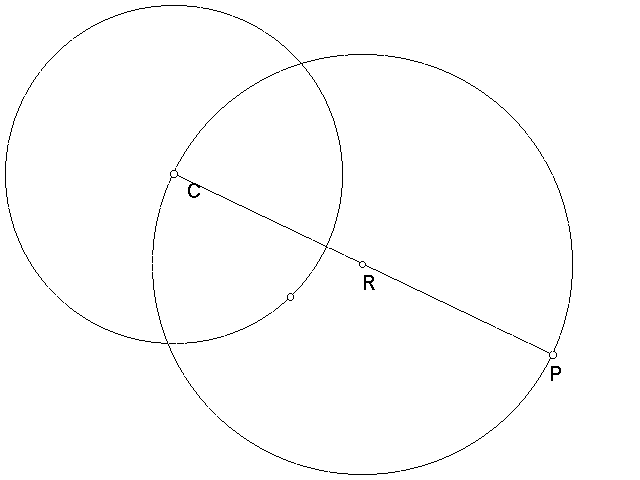
Notice that radius RP is the same as radius RC.

Step Five: Construct Rays from P to the points of intersections of the circles. You have now constructed two tangents to a circle through a rondom Point P.