Problem #91: Short Roads
There are four main towns in Lateralia. We will call them A, B, C and D.
They lie at the corners of a ten-mile square. In order to improve
communications between the towns, the Lateralian Department of Transport
decided to build a new road linking all four towns together. Because they had
very little money, it was decided that the new road system should be as short
as possible and still allow access from any one town to any other. The
engineers came up with three designs shown below.
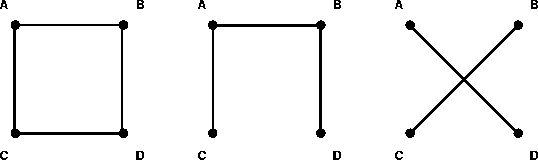
Number one uses 40 miles of
road, number two uses 30 miles of road, and number three uses 28.3 miles of
road. The designers naturally recommend plan number three because it employed
the smallest road area and, therefore, cost the least. However, when they
submitted their plan to the Minister of Finance, he accused them of
extravagance and quickly pointed out a better design that required even less
total road surface. What was his superior solution?
[Top |
Solution]

