Homework 7

1. Figure 1
   Orbifold notation: 3*3

   A three-way crossing point is at the point marked with a red dot. A three-fold gyration point is at the point marked with a blue dot.
   

   Figure 4
   Orbifold notation: 333

   The three types of three-fold gyration points are at the centers of each of the three different sized gray triangles.
   

   Figure 5
   Orbifold notation: *2222
   The four types of two-way crossing points are (1) near the chin, (2) near the forehead, (3) near the upper back of the head, and (4) near the lower back of the head.
   

   Figure 6
   Orbifold notation: 22*
   The two types of two-fold gyration points are at the points marked with green and red dots. There is one unique mirror line, which is marked in a couple of places in blue.
   

   Figure 7
   Orbifold notation: 4*2
   A four-fold gyration point is at the point marked with a red dot. A two-way crossing point is at any of the intersections of the blue lines.
   

   Figure 10
   Orbifold notation: 333
   The three types of three-fold gyration points are at (1) the centers of the red spirals, (2) the centers of the blue spirals, and (3) the center of the equilateral triangle formed by the centers of three adjacent points of type (1).
   

4. Design a pattern whose symmetry group has orbifold notation 2*22. You know from the in class exercise that it will have some lines of mirror reflection and that those lines will meet in pairs in two different ways. You also know that it has to have a gyration point at which it's symmetric under rotations of 2/2 radians (180 degrees), and that every gyration point and kaliedoscopic point in the pattern will be one of those mentioned above.

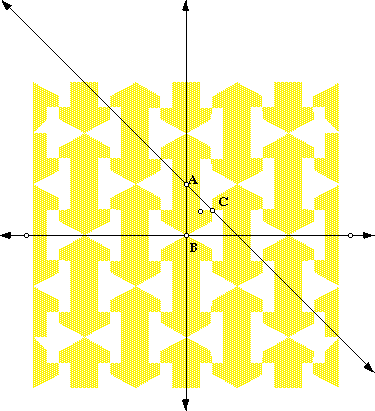
   Use The Geometer's Sketchpad to generate a picture of your pattern. Clearly label the two different types of kaleidoscopic point and the one type of gyration point.

   The figure on the left is from Geometer's Sketchpad (click on it to download the file) and the figure on the right is from Kali. Points A and B are the two different types of kaleidoscopic points and point C is the one type of gyration point.

   

6. Today's exercise made use of a Web page that wasn't written specifically for the course. The advantages of this are clear -- we avoided "re-inventing the wheel" by recycling someone else's work. The disadvantages are (hopefully) not as clear. Other peoples' Web pages can move, be deleted, or contain obscenities or copyright violations. Also, other peoples' pages generally aren't written for the precise grade level and topic that you want to teach.

   The ability to connect to and reference pages of others' work is one of the great strengths of hypertext documents. How would you deal with the weaknesses discussed above when producing your own Web pages? What other strengths and weaknesses of hypertext can you think of, and how might you exploit or avoid them in your own work? How can you configure your own Web pages to make them more useful to others who might want to refer to them? You may find yourself needing the answers to these questions when working on your final project!

   If a page contains a list of relevent links, then it should contain enough to still be useful a year later when 20% of the links no longer work. The links should also be carefully selected in terms of their predicted reliability. For example, linking to The Math Forum's list of geometry Web sites will probably be reliable, while linking Joe's little gallery of wallpaper may not.

   Another weakness of the web is that when you make a link to another site, there is more of a possiblity for the, um, "surfer" to get side tracked easily, because those other sites may have other links as well, and so on. A unit should be mostly self-contained but for a small section of "where to go from here." Another way to keep people from straying to far is to make use of certain HTML features, like the part of Netscape "frames" which allows you to put a tag in a hyper-link that will cause a new Web browser to be invoked on the new html page when the link is clicked on.

   Navigation links throughout a multipage HTML document are important. Since most Web traffic seems to come from search engines these days, often a person is thrown into the middle of a document without knowing what big picture of what they are looking at. "Up" or "Top" links are essential. "Next" and "Previous" links are helpful, though not as essential.

   The top page should be short and to the point. Choices of where to go to from the top page should be limited to probably about seven, and the decision about which choice to make (which link to follow) should be obvious (that's the goal, anyway).

Final Project Draft

See the unit on Symmetry.