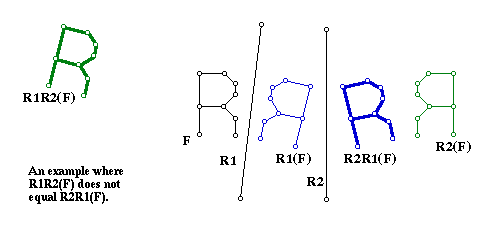
In the picture above, F is reflected across mirrors R1 and R2. It is plain to see that the order of reflection (which mirror first) can make a difference in the result. R1R2(F) does not equal R2R1(F) in this example, therefore R1R2 and R2R1 are not equivalent.
However, if the two mirror lines R1 and R2 are perpendicular to each other, then R1R2(F) = R2R1(F). This is illustrated in the example below.
The result of two reflections is a rotation about the intersection of the two mirror lines. If the two mirror lines are parallel (i.e. do not intersect), then the resulting tranformation is a translation. We know that the intersection is the center of rotation it is the only point which stays the same through both reflections. In a rotation, the only point which stays the same is the center. To find the angle of rotation of R1R2, call the intersection point of R1 and R2 I. Pick any point K not equal to I on R1, and any point M not equal to I on R2 [but on which side of R1, I don't know how to distinguish]. K stays the same when reflected across R1, but then rotates twice the angle of KIM when reflected across R2. Assuming the transformation is rigid, then the angle of rotation is twice the angle KIM. It follows then that under R2R1, the angle of rotation is the angle MIK, which is equal to -(angle KIM).
That is why when angle KIM = 90 degrees, R1R2(F) results in a 180 degree rotation and R2R1(F) results in a -180 degree rotation, which are equivalent. This also is demonstrated in the sketch below, but not very elegantly.
Examine this pattern -- can you find any rotational symmetries in it? Move your motif until copies of it form a ring around one of the corner points of your triangle. How many copies appear in that ring?
There is rotational symmetry at every corner of the triangle. There is 6-fold, 3-fold and 2-fold rotational symmetry at the 30 deg. corner, the 60 deg. corner and the 90 deg. corner, respectively. (There is also dihedral symmetry at each corner, but you didn't ask that.)At the 30 deg. corner, 12 copies of the motif appear in a ring. (6 copies at the 60 deg. and 4 copies at the 90 deg.) Since each copy is a reflection of the one next to it and only an even number of reflections restores the motif to its original orientation, all corners must show an even number of copies of the motif.
The angles between the mirrors were carefully chosen so that you would get a neat tiling of the plane. What properties must be satisfied for a triangle to generate such a nice pattern? Can you think of other polygons that might also generate such a pattern?
If we are just concerned with tiling around a single point, then any angle 180/n where n is an integer will fit nicely. Since as stated above there must be an even number of copies of the motif at each corner, the angle can be represented by 360 degrees divided by 2n (an even number), which simplifies to 180/n.Corners of 30, 60 and 90 degrees correspond to n = 6, 3 and 2 respectively. Using n=5, a corner of angle 180/n = 36 would fit around a point without overlapping.
However, to tile the plane with mirror-edged polygons, ALL corners of the polygon must be angles that are divisors of 180. Then, the maximum angle the polygon may have is 180/2 = 90 degrees.
The average interior angle of a triangle measures 60 degrees, so some triangles will work (we've seen some examples). The triangle must be either acute or right. The average interior angle of a quadralateral is 90 degrees, so some rectangles should work. However, the quadralateral must have all angles exactly equal to 90 degrees because making any one of them less than 90 would make another one greater than 90 (which is the max). Therefore only rectangles could work. The average interior angle of a n-gon where n>=5 is always greater than 90 degrees (180-360/n), so no n-gons where n>=5 may be used to tile this way - with mirrors on all sides.
So, the only polygons that would work are rectangles and acute or right triangles.
Since I'm not sure exactly the type of figure you had in mind, I made two.
More Symmetry Groups: pi/2, pi/2, pi/5
Basepoint: middle point of upper-left edge of triangleThis pentagonal prism is simple to make with one mirror on flat on the table and two perpendicular to the table but at a pi/5 angle with each other. Sticking a wedge of angle pi/5 between the mirrors gives creates the shape.
Symmetry Group: (2,3,5)
Basepoint: lower-left pointThis icosahedron can be created with two mirrors perpendicular to the table and the angle between them at pi/6. The third mirror goes at an angle from the table of about pi/3. The intersection of the third mirror and the table is perpendicular to one of the other mirrors. The surface of the table becomes the surface of the icosahedron.
Imagine you could draw in the Basepoint window the same way you can draw on the paper on your desk. Describe three properties you would expect to see if KaleidoTile could faithfully repeat your motif in its tiling.
- The pattern I draw should be repeated 20 times on the pentagonal prism and 120 times on the icosahedron (6 times on each of 20 faces).
- Each occurance of my pattern is adjacent to 3 copies of my pattern reflected across each of the three sides of the base triangle.
- As I draw near any of the borders of the triangle, the pattern I am making on the polyhedron will run into itself. As I draw near a corner, several copies of my pattern run into each other.
There are 4 combinations possible here:
- a paper handout for a hands-on activity,
- a paper handout for a computer activity,
- web page instructions for a hands-on activity, and
- web page instructions for a computer activity.
A disadvantage to using web page instructions for a computer activity is that there may not be enough space on the computer screen to see both the directions and the software at the same time. Flipping back and forth between windows can be a nuisance. There also may not be enough memory on the computer to run both at once. (More software bugs are revealed when a machine is heavily loaded than when it is lightly loaded.)
An advangage to using web page instructions for a computer activity or for a hands-on activity is that the teacher doesn't have to make as many handouts for students (perhaps if the copy machine is broken). Also, if the instructions for an activity are not exactly sequential (are more web like with optional tangents), then having them in web pages is quite beneficial.
An advantage to having instructions available on the World Wide Web (as opposed to just on local web pages) is that they are easily accessible to many more people than if they were just distributed in a book.
An advantage of having a paper handout for an activity is that students can write answers on the paper. Answers can be entered into "forms" on Web pages, but collecting them and correcting them requires additional effort (at least to initially set up).
As a student, I prefer using a handout to read instructions instead of reading from the computer. For whatever reason it is just more comfortable for me. I also prefer to write my answers on paper instead of typing them into the paper, even though I am a proficient typist. I prefer the looks of a type-written or web-page response, though.
As a teacher, I feel students should be given the choice of using the computer based instructions or a handout of the computer based instructions. I would like to collect answers on a piece of paper in the student's handwriting.
An ideal setup would be to have students work in pairs at a computer, one person reading the instructions on the handout, and the other running the software. Roles can be switched midway through the activity.
