Homework 3

Lori Thomson
(lori@geom.umn.edu)
Math 5337

Part A. Question 3 from Introduction to the Web Homework

See the source of this page or my home page.

Part B. Questions 4, 8 and 11 from Peaucelliers Linkage Homework

  1. Fill out the table in Part 2C.

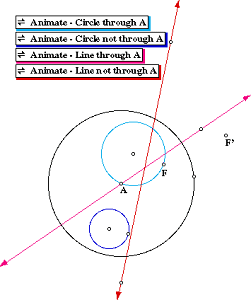
    Shape inverted Inverse of shape
    Circle through A Line not through A
    Circle not through A Circle not through A
    Line through A Line through A
    Line not through A Circle through A

    For a demonstration of each of these inversions, click on the sketch below.

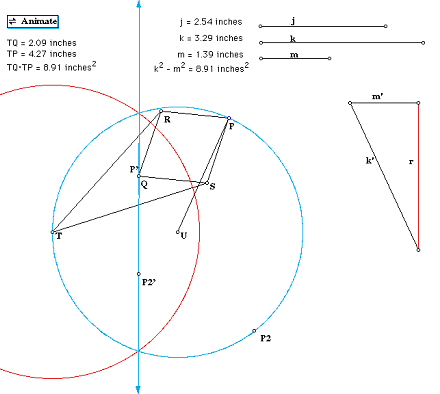
  2. Part 3B: What is the radius of the circle of inversion in terms of j, k, and m?
    Let r = the inversion radius. By dialation, r2 = (TQ)(TP).
    Let X be the midpoint of QP, and w = (RX). Then (QX) = (XP).
    By adding line segments,(TQ) = (TX) - (QX) and (TP) = (TX) + (QX).
    So (TQ)(TP) = [(TX) - (QX)] [(TX) + (QX)] = (TX)2 - (QX)2.
    By pythagorean theorem, (TX)2 = k2 - w2 and (QX)2 = m2 - w2.
    So now, (TQ)(TP) = (TX)2 - (QX)2 = (k2 - w2) - (m2 - w2) = k2 - m2.
    Thus, r2 = k2 - m2 and r = sqrt(k2 - m2).
    Explain how you can use segments of lengths j, k, and m to construct a segment of the length of the radius.
    To construct r, create a right triangle whose legs are lengths r and m and hypothenuse is length k (so that r2 = k2 - m2).
    1. Construct a circle with any center C and radius m.
    2. Create a segment m' of length m between the center and any point A on the circle.
    3. Construct a line l through A, perpendicular to m'.
    4. Construct a circle with center C and radius k.
    5. Construct a point B at the intersection of this circle and the line l.
    6. Complete the triangle by constructing segment r between A and B and segment k' between C and B.
    Create a Sketchpad sketch of Peaucellier's linkage which includes this circle of inversion.

  3. In standard Euclidean geometry, any pair of lines meets in one or no points. The shortest distance between two points is a straight line. Given a line and a point not on the line, there is exactly one line through that point which does not intersect the first line. (This is the famous "parallel postulate".)

    Inversion in the circle changes the objects we are familiar with in the Euclidean plane, and changes the relations between them. For instance, the inverse of a pair of parallel lines is a pair of circles that meet at the center of the circle of inversion. Other relations between objects stay the same: exercise 10 shows that inversion preserves angles if the "angle between two circles" is correctly defined.

    Choose some familiar definition, axiom, or theorem from Euclidean geometry and explore its manifestation in an inverted Euclidean geometry. Discuss the consequences of any changes you discover.

    For instance, the definition of "line" might be changed to mean "infinite straight objects and circles through the origin". This would have consequences for all axioms and theorems about lines. "Triangles" would no longer have straight line segments for sides, but the sum of their angles would still be 180 degrees. In an inverted geometry, statements about similarity and congruence of triangles become much more complicated.

In standard Euclidean geometry, a triangle is composed of three line segments. When the triangle is inverted in a circle, it becomes three arcs. The Pythagorean theorem still holds true for the length of the arcs. [...]

Part C. Questions 1, 2 and 3 from Warm up questions of the Dynamical systems lab.

  1. Suppose we have a dynamical system given by the square root function on your calculator. Type in any number and calculate its square root. Take the square root of the result. Take the square root again and so on. Give a full description of the dynamics, similar to what was done for the racoon model.
    For the function f(x) = sqrt(x), a typical orbit will look like one of the following:
    100, 10, 3.1623, 1.7783, 1.3335, 1.1548, 1.0747, 1.0366, ..., 1.0000...
    or .5, 0.707, 0.8409, 0.9170, 0.9576, 0.9786, 0.9892, 0.9946, 0.9999...
    The only fixed points are 0 and 1, where 0 is repelling and 1 is attracting (from both directions). All iterations will eventually go to 1, independent of the initial state (negative initial states and complex solutions not considered).

  2. What happens if you use a function other than the square root function? Give a description of the dynamics for a dynamical system given by the consine button.
    For the function f(x) = cos(x), where x is in radians, orbits alternate above and below the fixed point 0.73908513 getting closer and closer. Fro example:
    1, 0.5403, 0.8576, 0.6543, 0.7935, ..., 0.73908513
    Graphing the intersection of y = x and y = cox(x) shows that this is the only fixed point for this function, and it is attracting. All iterations eventually end up at 0.73908513, independent of initial state.

  3. Describe the dynamics of the +/- button.
    For the function f(x) = -x, the only fixed point is 0, which is neither attracting or a repelling. 0 is the only initial state which will ever lead to 0. All other states will alternate above and below 0 and never converge.