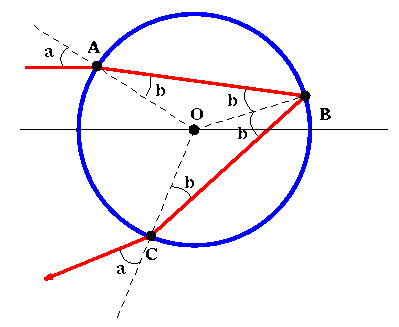
Figure 3: Ideal path of a light ray through a spherical water droplet.
Dashed lines represent normals.

In this section we will build on our previous work to compute the rainbow angle. If rays of sunlight are traveling parallel to each other (which may be assumed on Earth), then the rainbow angle is the angle in the sky at which rainbows appear to observers on Earth's surface. Along the way we will examine what makes a rainbow. This simulation lets you follow rays of light as they are refracted (by obeying Snell's Law) and reflected (by obeying the Law of Reflection) in a raindrop.
In Figure 3 we depict a light ray hitting a water droplet at point A. Some of the light will be reflected and some of the light will enter the droplet. The light that enters will be refracted as discussed in the previous section. It then hits the other side of the droplet at point B where some of it will exit and the rest will reflect back. Finally at point C some of the light will exit and be seen by an observer.

To run this experiment you need to use the interactive Internet Web site http://www.geom.umn.edu/education/calc-init/rainbow/rainbow.cgi. There you are able to experiment with "shooting" rays of light into a water droplet. The beam of light enters the water droplet at some height as measured from the droplet's center. This height is called the impact parameter, w. In Figure 3, the central horizontal line represents w = 0, the top of the water droplet represents w = 1, and the bottom of the water droplet represents w = -1. Each time you run the simulation, it will calculate what angle the light leaves the water droplet at as measured from the horizontal. This angle is called the deflection angle, D. The deflection angle is measured as the (obtuse) angle between the light ray exiting the droplet and the central horizontal line.
Run the following experiments and answer the questions using the information you gather from simulations.
Experiment #1For the purpose of the first two experiments, you may ignore the "wavelength" of light rays. For best "experimental data," set the "wavelength" to be 700 nanometers (red light). (We will look at the effect of wavelength later.)
|
Experiment #2The next activity will help you answer the question "When will incoming light be focused most intensely?" In other words, when will a range of incoming rays all leave the droplet at approximately the same angle?
|
| Impact Parameter w | Deflection at w D(w | Deviation from w
| Deflection at w + + w wD(w | Relative Change in Deflection![{D(w0+[delta]w)-D(w0)}/{[delta]w}](def.gif)
|
| 0.10 | _________ | -0.05 | _________ | _________ |
| 0.10 | _________ | +0.05 | _________ | _________ |
| 0.55 | _________ | -0.05 | _________ | _________ |
| 0.55 | _________ | +0.05 | _________ | _________ |
| 0.80 | _________ | -0.05 | _________ | _________ |
| 0.80 | _________ | +0.05 | _________ | _________ |
Experiment #3
|
