Rainbow Lab
Part 1 - Preparation
How are rainbows formed? Why do they only occur when
the sun is behind the observer? If the sun is low on the
horizon, at what angle in the sky should we expect to see
a rainbow? This lab helps to answer these and other questions by examining a mathematical model of light
passing through a water droplet.
| 
|
To understand how a rainbow forms, we need to recall two important laws that explain the behavior of light rays.
| 1. Law of Reflection: The angle of incidence is equal to the angle of reflection.
For the figure at right,
angle(a) = angle(b).
| 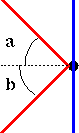
Figure 1: The reflection of light from a smooth surface.
|
|
2. Snell's Law / Law of Refraction: The ratio of the
sine of the angle of incidence to the sine of the angle of refraction is
a constant. This constant is the ratio of the speed of light in the "incident" medium to the speed of light in the "refracting" medium.
For the figure at right,
sin(a)/sin(b) = (speed of light in air)/(speed of light in water).
The speed of light in air depends on the temperature and pressure of the
air, and similarly for water and other medium. By contrast the speed
of light in a vacuum is an absolute constant, which we represent by
c.
| 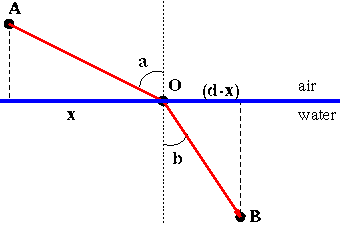
Figure 2: A light ray passing from air into water.
|
The index of refraction for substances is the ratio
c/v where v is the speed of light in that medium.
The table below has been compiled for the ratio of the
speed of light in a vacuum to that of various other mediums.
Indices of Refraction (n)
for yellow light with a wavelength of 589 nm
| Material | n = c/v
|
| Air (at STP) | 1.0003
|
| Water | 1.33
|
| Ethyl Alcohol | 1.36
|
| Glass:
|
Fused quartz| 1.46
| |
Crown glass| 1.52
| |
Light flint| 1.58
| |
| Lucite or Plexiglass | 1.51
|
| Sodium chloride | 1.53
|
| Diamond | 2.42
|
Since the index of refraction of air is nearly 1, when light is traveling from air into another medium, Snell's law is approximately: sin(a)/sin(b) = n, where a is the angle of incidence, b is the angle of refraction, and n is the index of refraction of the other medium.
Question 1Note that the Law of Reflection and Snell's Law
do not depend on the direction of the light ray. That is, our results
would have been identical if we had assumed that the source of
light was the point B instead of A. With this observation,
answer the following questions:
- If a medium has a large index of refraction, what does that say
about the speed of light in that medium?
- If light travels from one medium to another of
higher refractive index, what can you say about the way the light ray
bends in relation to the perpendicular line to the surface
between the media? This perpendicular line is called the "normal".
- What happens when light travels to a medium
of lower refractive index, both in terms of speed and the way it bends?
|
Question 2 Experimentally it may be difficult to measure
the angle of refraction for a crystal with an unknown index of refraction.
- Given a "slab" of crystal of thickness, T, draw a diagram
that depicts the passage of light through the crystal.
- What is the relationship between the angle of incidence and the angle to the normal at which the light ray leaves the crystal?
- Design a method to experimentally
determine the angle of refraction in the crystal in terms of T.
|
Suppose we experimentally determine the index
of refraction for some crystal by accurately measuring the angle of
refraction, b , that occurs when incoming light travels through a
vacuum and strikes the crystal at an angle of incidence equal to a , that occurs when incoming light travels through a
vacuum and strikes the crystal at an angle of incidence equal to a .
Suppose now we slightly change the direction of the oncoming light
so that the angle of
incidence is now a = a .
Suppose now we slightly change the direction of the oncoming light
so that the angle of
incidence is now a = a + +  a, where a, where  a is the change in the angle of incidence. To estimate
the new angle of refraction, b, think of b as a function of a and write it as b(a) = b(a a is the change in the angle of incidence. To estimate
the new angle of refraction, b, think of b as a function of a and write it as b(a) = b(a + +  a) = b(a a) = b(a ) + ) +  b. At this point, caclulus is required to derive the estimation b. At this point, caclulus is required to derive the estimation  b b  b'(a b'(a ) ) a when a when  a is small, where b'(a a is small, where b'(a ) = ) = ![[cos(<em>a0</em>)]/[<em>i</em>*cos(<em>b0</em>)]](eq.gif) . Combining these gives . Combining these gives
b(a)  b(a b(a ) + ) + ![[cos(<em>a0</em>)]/[<em>i</em>*cos(<em>b0</em>)]](eq.gif)  a. a.
Question 3
- Use the above equation to estimate the angle of refraction when
a
 = 45°, = 45°,  a = 5°, and the crystal is diamond. (You will need to look up the index of refraction for
diamond in the index of refraction table.) a = 5°, and the crystal is diamond. (You will need to look up the index of refraction for
diamond in the index of refraction table.)
- Use Snell's Law to compute the actual angle of refraction for diamond for a 50°
angle of incidence. How close was your estimate to the actual
answer?
- Repeat questions 3a and 3b for
 a = 20°. Is your estimate better or worse in this case? Why? a = 20°. Is your estimate better or worse in this case? Why?
|

| 


 , that occurs when incoming light travels through a
vacuum and strikes the crystal at an angle of incidence equal to a
, that occurs when incoming light travels through a
vacuum and strikes the crystal at an angle of incidence equal to a a, where
a, where  b'(a
b'(a![[cos(<em>a0</em>)]/[<em>i</em>*cos(<em>b0</em>)]](eq.gif) . Combining these gives
. Combining these gives