
This page lists a number of infinite expressions of  . Proofs are not provided here, but the viewer is encouraged to study the sources listed in the reference page.
. Proofs are not provided here, but the viewer is encouraged to study the sources listed in the reference page.
![INTEGRAL{0...1}Squareroot[1-x^2]dx = pi/4](eq5.gif)
and without using the binomial theorem or integration (not invented yet) painstakingly came up with a formula for  to be
to be
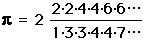 .
.
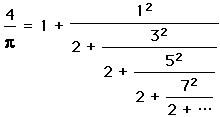 .
.
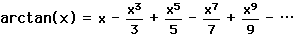 ,
,
and the fact that arctan(1) =  /4 to obtain the series
/4 to obtain the series
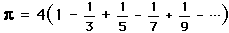 .
.
Unfortunately, this series converges to slowly to be useful, as it takes over 300 terms to obtain a 2 decimal place precision. To obtain 100 decimal places of  , one would need to use at least 10^50 terms of this expansion!
, one would need to use at least 10^50 terms of this expansion!
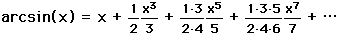 ,
,
and the fact that arctan(1/2) =  /6 to obtain the series
/6 to obtain the series
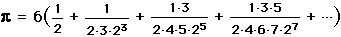 .
.
This arcsine series converges much faster than using the arctangent. (Actually, Newton used a slightly different expansion in his original text.) This expansion only needed 22 terms to obtain 16 decimal places for  .
.
 ,
,
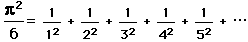
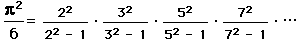
 in terms of the Fibonacci numbers,
in terms of the Fibonacci numbers,
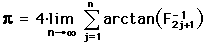 .
.
Return to Historical Overview of Pi

http://www.geom.umn.edu/~huberty/math5337/groupe/expresspi.html Copyright © 1996-1997 Michael D. Huberty, Ko Hayashi & Chia Vang
Created: March 1996 ---- Last Modified: July 6, 1997