Curve Shrinking,
Star Shapes,
&
Sliding Octagons
by
Michael D. Huberty
The Geometry Center
University of Minnesota
Summer 1991
Contents
- Introduction
- Curve Shrinking
- Star Shapes
- Sliding Octagons
- Conclusion
Introduction
This summer I worked at the Geometry Center studying different geometric phenomena. I wanted to take advantage of the computing facilities and the staff available at the Geometry Center. The goal I set for myself was to learn as much as I could about mathematics and computing and to use this knowledge to help others better understand mathematical concepts.
During the first couple of weeks I learned how to use the computers and software. A also attended the course Geometry and
the Imagination taught by Professors Conway, Doyle, Gilman, and Thurston from Princton University. I learned more from this course than any other course I have taken in my academic career. It was fascinating to learn about different polyhedra, curvature, and spherical and hyperbolic geometries.
I spent most of my time this summer working in the following areas: curvature and curve shrinking, star shaped polygons and curves, and sliding regular polygons. Most of my learning discoveries and observations came from programming using Mathematica (version 1.2) and reading literature on my subjects.
I would like to thank Stan Wagon, Jeff Ondich, and Anthony Iano-Fletcher for their help on my projects.
Curve Shrinking
My main project was working on the following theorem:
Theorem 1: Suppose each point along a non-self-intersecting, closed curve moves along the path perpendicular to the tangent to the curve at that point at a rate proportional to the curvature at the point (Figure 1). Then the curve tends to a circle. ×
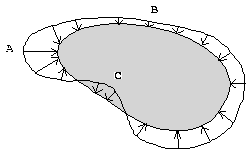 Figure 1: Illustrating Theorem 1. Region A on the curve has large
curvature, so the points move inward a large amount.
The points of region B move inward a small amount due
to small curvature. Region C has negative curvature, so
the points move outward.
Figure 1: Illustrating Theorem 1. Region A on the curve has large
curvature, so the points move inward a large amount.
The points of region B move inward a small amount due
to small curvature. Region C has negative curvature, so
the points move outward.
The literature on this subject was very difficult to understand. With the help of Jeff Ondich I managed to modify a proof by Michael Gage which almost proves this theorem for closed curves which are continuously once differentiable and piecewise twice differentiable.
I wanted to write a program using Mathematica that would simulate this process of shrinking a curve to a circle. This was difficult to do since this process is continuous, but computers work in discrete steps. Also, once the points on the curve have moved some distance, I no longer would have an equation for the resulting curve. I quickly realized that I would need to look at the paths of certain points on the curve. I.e. I would have to allow flexability in my program for the user to define how large each step in the shrinking process would be for any input curve. For example, a shape which is nearly square will evolve into a circle is shown in Figures 2-4.
I allowed different graphic output forms, so the information could be viewed in different ways. One output form is to produce many sequential pictures thich can then be viewed as an animation (Figure 2). each frame also displays the isoperimetric ratio L^2/A, where L is the arclength and A is the area of the curve. For any closed curve, L^2/A is greater than or equal to 4*pi. The equality L^2=4*pi holds only for a circle. Thus as a curve evolves in this shrinking process in the theorem, L^2/A approaches 4*pi. Because this ratio is displayed, this form of output is the most informative. The fifth image in Figure 2 not only looks like a circle, but L^2/A is very close to 4*pi.

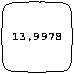

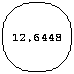
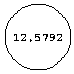 Figure 2: Shrinking of a square.
Figure 2: Shrinking of a square.
The second form of output is to show where point on the original curve go during this process (Figure 3). The final type of output is to show the process in three dimensions by stacking each frame of the process, one on top another (Figure 4).

 Figure 3: Shrinking of a square Figure 4: Shrinking of a square
- follow points. - stacked in 3-D.
Figure 3: Shrinking of a square Figure 4: Shrinking of a square
- follow points. - stacked in 3-D.
Star Shapes
A point in the enclosed region of a polygon (or a closed curve) is called a star center if every line segment from that point to the polygon (or curve) lies within the enclosed region. A star shaped polygon (or curve) is a polygon (or closed curve) with at least one star center (Figure 5). If every point in the region enclosed by a closed curve is a star center, then the curve is called convex/ (The gray shaded curve of Figure 1 is convex, while the other curve in that picture is not convex.)
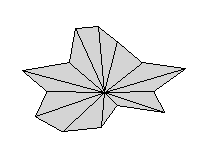
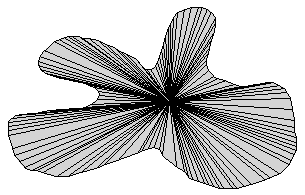 Figure 5: Star shaped polygon and curve with line segments
emanating from a star center.
Figure 5: Star shaped polygon and curve with line segments
emanating from a star center.
Stan Wagon introduced the following theorem to me which I proved for both polygons and curves:
Theorem 2: Given any star shaped polygon (or curve), there exists a finite length that can be added on to each line segment from the star center to a vertex of the polygon (or a point on the curve) such that the new polygon (or curve) consisting of points at the ends of these extended line segments is convex. ×
I wrote a Mathematica program that would take any star polygon with a given star center and (1) add on any given distance to each ray from the center, or (2) it would calculate a sufficient distance to add on to each ray to make the resulting object convex. This calculated distance is certainly not the "best" distance to make the object convex. Usually this calculation produces a number so large that the resulting convex polygon is orders of magnitude larger than needed to become convex. To use this program with a curve, one can use many points of the curve and consider it to be a polygon.
I again allowed for different ways to display this. Figure 6 shows the original polygon, its convex counterpart, and the rays from a star center outward. Adding on a given distance to the previous frame sequentially shows what happens to the shape as it is expanded. By doing this it is also possible to see what happens if different star centers are used. Figure 7 shows the expansion of a curve for different star centers
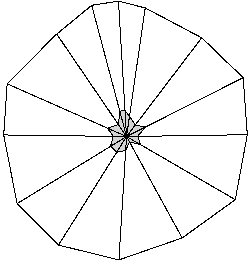 Figure 6: Expansion of a star shaped polygon to a convex polygon.
Figure 6: Expansion of a star shaped polygon to a convex polygon.
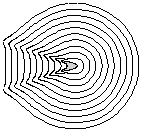
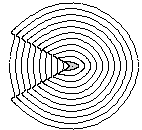 Figure 7: The left picture shows the expansion of a curve with
the star center at the right end. The right picture has
the star center near the center of the curve.
Figure 7: The left picture shows the expansion of a curve with
the star center at the right end. The right picture has
the star center near the center of the curve.
Sliding Octagons
Peter Doyle from Princeton contacted me about animating a theorem of his. In addition, Max Karoubi from Paris, the founder of the European Congress of Mathematics (ECM), wanted to use Doyle's theorem as a logo for the ECM. The theorem is the following:
Theorem 3: Three octagons of radius 1/2+1/(2*sqrt(2)) perfectly fit inside a larger octagon of radius 3/2+1/(2*sqrt(2)). In addition, these three octagons slide around (one or two at a time) inside the larger octagon with their centers traveling on the edge of an octagon of radius 1. The region inside the large octagon which is never touched by the three sliding octagons is a center octagon of radius 1/2-1/(2*sqrt(2)). ×
I used Mathematica to create an animation of these octagons sliding around. Figure 8 shows a few frames from this animation. In addition, I made another animation of this, but using the letters E, C, M instead of the octagons (Figure 9). A single fram of the latter animation will be used by the ECM as their logo, colored blue, red, and white for the French flag. [Editor's Note: For political reasons, the logo was never used. - MDH]
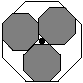
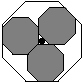
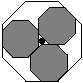
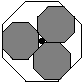
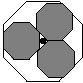 Figure 8: Sliding octagons.
Figure 8: Sliding octagons.
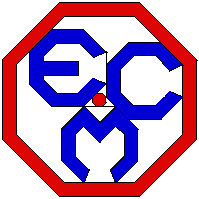 Figure 9: ECM logo.
Figure 9: ECM logo.
Conclusion
My work at the Geometry Center has been worth every minute. It has given me the chance to research and learn geometry in a way I would otherwise not have had the opportunity to do. I also feel I have gained knowledge from my coworkers' projects. I feel I have contributed to the Center and to others, such as my coworkers and even Peter Doyle.
I plan on continuing to work with Doyle on some other questions regarding regular polygons sliding inside larger regular polygons. Doyle's theorem about the sliding octagons also applies to squares. However, Doyle believes it only applies to squares and octagons. He would like me to try to prove that. [Editor's Note: This never happened. - MDH]

http://www.geom.umn.edu/~huberty/Summer91/shortpaper.html
Created: October, 1995 ---- Last Modified: July 16, 1997
Copyright © 1991, 1995-1997 Michael D. Huberty
 Figure 1: Illustrating Theorem 1. Region A on the curve has large
curvature, so the points move inward a large amount.
The points of region B move inward a small amount due
to small curvature. Region C has negative curvature, so
the points move outward.
Figure 1: Illustrating Theorem 1. Region A on the curve has large
curvature, so the points move inward a large amount.
The points of region B move inward a small amount due
to small curvature. Region C has negative curvature, so
the points move outward.


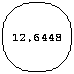
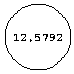 Figure 2: Shrinking of a square.
Figure 2: Shrinking of a square.

 Figure 3: Shrinking of a square Figure 4: Shrinking of a square
- follow points. - stacked in 3-D.
Figure 3: Shrinking of a square Figure 4: Shrinking of a square
- follow points. - stacked in 3-D.

 Figure 5: Star shaped polygon and curve with line segments
emanating from a star center.
Figure 5: Star shaped polygon and curve with line segments
emanating from a star center. Figure 6: Expansion of a star shaped polygon to a convex polygon.
Figure 6: Expansion of a star shaped polygon to a convex polygon.

 Figure 7: The left picture shows the expansion of a curve with
the star center at the right end. The right picture has
the star center near the center of the curve.
Figure 7: The left picture shows the expansion of a curve with
the star center at the right end. The right picture has
the star center near the center of the curve.




 Figure 8: Sliding octagons.
Figure 8: Sliding octagons.
 Figure 9: ECM logo.
Figure 9: ECM logo.