Geometry Lab: Medians of Triangles
Suppose we have a triangle ABC with its medians included
as the following picture shows. Recall that a median of a triangle
is a segment which starts at one vertex and ends at the midpoint of the
opposite side.
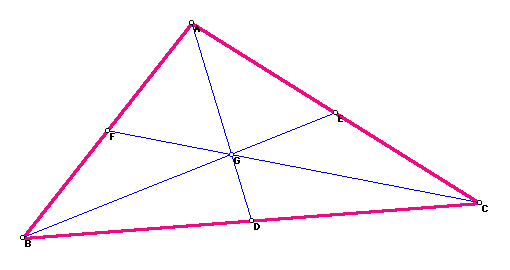
In this lab you will need to launch the Geometer's Sketchpad
program to discover some facts about medians of triangles.
Have someone in your group write out answers to the following questions:
Questions
- Problem #1
- From looking at this picture, it appears that the three medians
all intersect at the same point G. Do you think this occured
because we picked a special triangle, or do you think the medians
would intersect at the same point for any triangle? Why or why not?
Hint: In the Sketchpad program vary the length of the sides AB, BC and CA.
- Problem #2
- Using the Sketchpad program measure the length of the segment AG
and then the length of the segment AD. What is the ratio of these two
segments? Vary the length of the sides of the triangle. How does this affect
the ratio?
- Problem #3
- Repeat Question #2 with the segments BG and BE. What do
you observe? What would the result be if you were to repeat Question #2
with the segments CG and CF?
- Problem #4
- From the results of the earlier problems, can you make a conjecture or
conjectures about properties of the medians of triangles? Along with
these conjectures, some mathematical justification should be included.
The following list of hints may be useful, but should
only be used if needed.
Introductory Page

